题目描述
一张地图上有n个城市,城市和城市之间有且只有一条道路相连:要么直接相连,要么通过其它城市中转相连(可中转一次或多次)。城市与城市之间的道路都不会成环。
当切断通往某个城市 i 的所有道路后,地图上将分为多个连通的城市群,设该城市i的聚集度为DPi(Degree of Polymerization),DPi = max(城市群1的城市个数,城市群2的城市个数,…城市群m 的城市个数)。
请找出地图上DP值最小的城市(即找到城市j,使得DPj = min(DP1,DP2 … DPn))
提示:如果有多个城市都满足条件,这些城市都要找出来(可能存在多个解)
提示:DPi的计算,可以理解为已知一棵树,删除某个节点后;生成的多个子树,求解多个子数节点数的问题。
输入描述
每个样例:第一行有一个整数N,表示有N个节点。1 <= N <= 1000。
接下来的N-1行每行有两个整数x,y,表示城市x与城市y连接。1 <= x, y <= N
输出描述
输出城市的编号。如果有多个,按照编号升序输出。
用例
| 输入 | 5 1 2 2 3 3 4 4 5 |
| 输出 | 3 |
| 说明 |
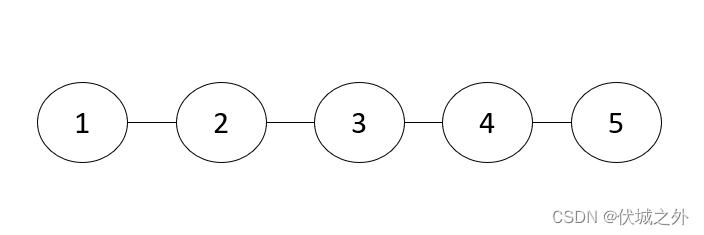
输入表示的是如下地图:
对于城市3,切断通往3的所有道路后,形成2个城市群[(1,2),(4,5)],其聚集度分别都是2。DP3 = 2。 对于城市4,切断通往城市4的所有道路后,形成2个城市群[(1,2,3),(5)],DP4 = max(3,1)= 3。 依次类推,切断其它城市的所有道路后,得到的DP都会大于2,因为城市3就是满足条件的城市,输出是3。 |
| 输入 | 6 1 2 2 3 2 4 3 5 3 6 |
| 输出 | 2 3 |
| 说明 | 将通往2或者3的所有路径切断,最大城市群数量是3,其他任意城市切断后,最大城市群数量都比3大,所以输出2 3 |
题目解析
用例1的意思如下:
DPi = max(城市群1的城市个数,城市群2的城市个数,…城市群m 的城市个数)
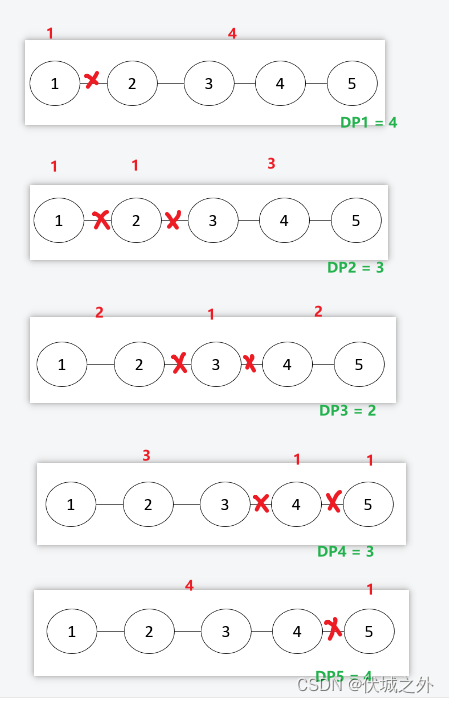
题目要求找出地图上DP值最小的城市(即找到城市j,使得DPj = min(DP1,DP2 … DPn)),
因此DP3最小,输出DP3的3。
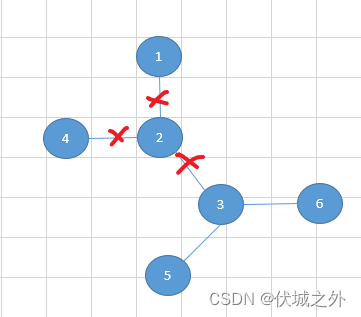
用例2图示如下
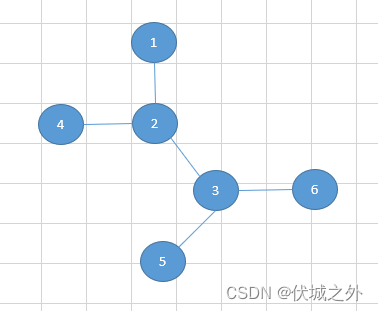

输出2,3。
通过上面两个示例的图示可以发现,其实本题就是求解:图的连通分量。
本题的难点在于,分量关系没有直接给出,需要我们自己推导,其次是需要我们统计出每个连通分量的节点个数。
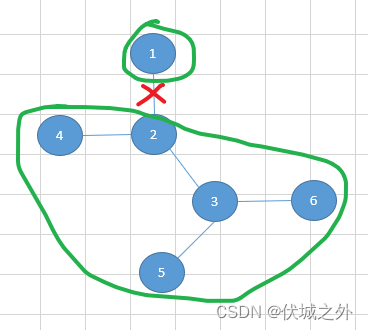
比如,上面且1的所有联系,则会产生两个连通分量,分别是[1], [4,2,3,5,6],这两个连通分量的节点个数分别为1,5。
求解图的连通分量,我们一般使用并查集。
但是,这里我们不能直接根据输入的连接关系,来产生并查集,因为输入的连接关系没有被切断。
本题是要我们尝试切断每一个城市的连接,因此我们遍历出每一个城市,比如城市2,然后遇到和城市2相关的连接后,我们就跳过并查集的合并操作,这样就能产生切断效果。
我们模拟下用例2
初始时,每个城市的父都是自己
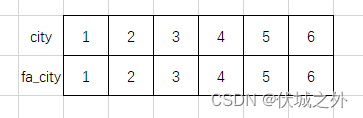
输入的连接关系如下
1 2
2 3
2 4
3 5
3 6
现在我们要切断城市2的所有联系,则遇到和2相关的连接时就不进行合并操作
因此上述连接关系只需要考虑
3 5
3 6
这样的话,最终并查集的合并结果为
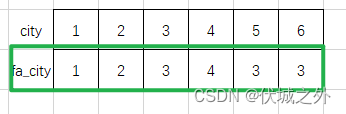
可以发现,父为3的连通分量具有最多城市数量
这样的话,我们就可以求解出每个DPi了,最后求其中最小的DP对应i即可。
JavaScript算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const n = parseInt(await readline());
const relations = [];
for (let i = 0; i < n - 1; i++) {
relations.push((await readline()).split(" ").map(Number));
}
console.log(getMinDP(relations, n));
})();
function getMinDP(relations, n) {
// minDp用于保存最小城市聚集度
let minDp = Infinity;
// city用于保存最小城市聚集度对应的被切割的城市序号
let city = [];
// 遍历每个城市 1~n
for (let i = 1; i <= n; i++) {
// 利用并查集对城市进行关联
const ufs = new UnionFindSet(n + 1);
for (let [x, y] of relations) {
// 切断城市的所有道路,即忽略和城市i有联系的合并操作
if (x === i || y === i) continue;
// 否则连接x和y
ufs.union(x, y);
}
// 统计各个连通分量自身的城市个数
const cnts = new Array(n + 1).fill(0);
for (let j = 1; j <= n; j++) {
const fa = ufs.find(j);
cnts[fa]++;
}
// 取最多城市个数作为当前的切断城市的聚集度
const dp = Math.max(...cnts);
if (dp < minDp) {
minDp = dp;
city = [i];
} else if (dp === minDp) {
city.push(i);
}
}
// 如果有多个,按照编号升序输出。
city.sort((a, b) => a - b);
return city.join(" ");
}
/* 并查集 */
class UnionFindSet {
constructor(n) {
this.fa = new Array(n).fill(0).map((_, idx) => idx);
}
find(x) {
if (x !== this.fa[x]) {
return (this.fa[x] = this.find(this.fa[x]));
}
return x;
}
union(x, y) {
let x_fa = this.find(x);
let y_fa = this.find(y);
if (x_fa !== y_fa) {
this.fa[y_fa] = x_fa;
}
}
}
Java算法源码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
import java.util.StringJoiner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] relations = new int[n - 1][2];
for (int i = 0; i < n - 1; i++) {
relations[i][0] = sc.nextInt();
relations[i][1] = sc.nextInt();
}
System.out.println(getResult(n, relations));
}
public static String getResult(int n, int[][] relations) {
// 记录最小dpi
int minDp = Integer.MAX_VALUE;
// 记录最小dpi对应的切断城市
ArrayList<Integer> city = new ArrayList<>();
// i 是被切断城市
for (int i = 1; i <= n; i++) {
// 利用并查集对城市进行关联
UnionFindSet ufs = new UnionFindSet(n + 1);
for (int[] relation : relations) {
int x = relation[0];
int y = relation[1];
// 如果x或y是被切断城市,则对应连接关系不成立
if (x == i || y == i) continue;
// 否则连接x和y
ufs.union(x, y);
}
int[] cnts = new int[n + 1];
for (int j = 1; j <= n; j++) {
// 对j=1~n每个城市找根fa
int fa = ufs.find(j);
// 根fa下的子城市个数++
cnts[fa]++;
}
// cnts的最大值即最大城市群大小
int dp = Arrays.stream(cnts).max().orElse(0);
// 和minDp比较,保留最小值
if (dp < minDp) {
minDp = dp;
city = new ArrayList<>();
city.add(i);
} else if (dp == minDp) {
city.add(i);
}
}
// 如果有多个,按照编号升序输出。
city.sort((a, b) -> a - b);
StringJoiner sj = new StringJoiner(" ");
for (Integer c : city) {
sj.add(c + "");
}
return sj.toString();
}
}
// 并查集实现
class UnionFindSet {
int[] fa;
public UnionFindSet(int n) {
this.fa = new int[n];
for (int i = 0; i < n; i++) fa[i] = i;
}
public int find(int x) {
if (this.fa[x] != x) {
return this.fa[x] = this.find(this.fa[x]);
}
return x;
}
public void union(int x, int y) {
int x_fa = this.find(x);
int y_fa = this.find(y);
if (x_fa != y_fa) {
this.fa[y_fa] = x_fa;
}
}
}
Python算法源码
import sys
# 输入获取
n = int(input())
relations = [list(map(int, input().split())) for i in range(n - 1)]
# 并查集
class UnionFindSet:
def __init__(self, n):
self.fa = [i for i in range(n)]
def find(self, x):
if x != self.fa[x]:
self.fa[x] = self.find(self.fa[x])
return self.fa[x]
return x
def union(self, x, y):
x_fa = self.find(x)
y_fa = self.find(y)
if x_fa != y_fa:
self.fa[y_fa] = x_fa
# 算法入口
def getResult():
# minDp用于保存最小城市聚集度
minDp = sys.maxsize
# city用于保存最小城市聚集度对应的被切割的城市序号
city = []
# 遍历每个城市 1~n
for i in range(1, n + 1):
# 利用并查集对城市进行关联
ufs = UnionFindSet(n + 1)
for x, y in relations:
# 切断城市的所有道路,即忽略和城市i有联系的合并操作
if x == i or y == i:
continue
# 否则连接x和y
ufs.union(x, y)
# 统计各个连通分量自身的城市个数
cnts = [0] * (n + 1)
for j in range(1, n + 1):
fa = ufs.find(j)
cnts[fa] += 1
# 取最多城市个数作为当前的切断城市的聚集度
dp = max(cnts)
if dp < minDp:
minDp = dp
city = [i]
elif dp == minDp:
city.append(i)
# 如果有多个,按照编号升序输出。
city.sort()
return " ".join(map(str, city))
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
/** 并查集定义 **/
typedef struct {
int *fa;
} UFS;
UFS *new_UFS(int n) {
UFS *ufs = (UFS *) malloc(sizeof(UFS));
ufs->fa = (int *) malloc(sizeof(int) * n);
for (int i = 0; i < n; i++) {
ufs->fa[i] = i;
}
return ufs;
}
int find_UFS(UFS *ufs, int x) {
if (x != ufs->fa[x]) {
ufs->fa[x] = find_UFS(ufs, ufs->fa[x]);
return ufs->fa[x];
}
return x;
}
void union_UFS(UFS *ufs, int x, int y) {
int x_fa = find_UFS(ufs, x);
int y_fa = find_UFS(ufs, y);
if (x_fa != y_fa) {
ufs->fa[y_fa] = x_fa;
}
}
int cmp(const void *a, const void *b) {
return (*(int *) a) - (*(int *) b);
}
/** 算法入口 **/
int main() {
int n;
scanf("%d", &n);
int relations[n - 1][2];
for (int i = 0; i < n - 1; i++) {
scanf("%d %d", &relations[i][0], &relations[i][1]);
}
// 记录最小dpi
int minDp = INT_MAX;
// 记录最小dpi对应的切断城市
int city[n];
int city_size = 0;
// i 是被切断城市
for (int i = 1; i <= n; i++) {
// 利用并查集对城市进行关联
UFS *ufs = new_UFS(n + 1);
for (int j = 0; j < n - 1; j++) {
int x = relations[j][0];
int y = relations[j][1];
// 如果x或y是被切断城市,则对应连接关系不成立
if (x == i || y == i) continue;
// 否则连接x和y
union_UFS(ufs, x, y);
}
// cnts记录每个根(每个节点都能当成一个根来看)下的城市个数
int cnts[n + 1];
for (int k = 0; k <= n; k++) {
cnts[k] = 0;
}
for (int k = 1; k <= n; k++) {
// 对k=1~n每个城市找根fa
int fa = find_UFS(ufs, k);
// 根fa下的子城市个数++
cnts[fa]++;
}
// cnts的最大值即最大城市群大小
int dp = cnts[1];
for (int k = 2; k <= n; k++) {
if (cnts[k] > dp) {
dp = cnts[k];
}
}
// 和minDp比较,保留最小值
if (dp < minDp) {
minDp = dp;
city_size = 0;
city[city_size++] = i;
} else if (dp == minDp) {
city[city_size++] = i;
}
}
// 如果有多个,按照编号升序输出。
qsort(city, city_size, sizeof(int), cmp);
for (int i = 0; i < city_size; i++) {
printf("%d", city[i]);
if (i != city_size - 1) {
printf(" ");
}
}
return 0;
}免责声明:
评论0