题目描述
A、B两个人玩抢7游戏，游戏规则为：
A先报一个起始数字 X（10 ≤ 起始数字 ≤ 10000），B报下一个数字 Y （X – Y < 3），A再报一个数字 Z（Y – Z < 3），以此类推，直到其中一个抢到7，抢到7即为胜者；
在B赢得比赛的情况下，一共有多少种组合？
输入描述
起始数字 M
- 10 ≤ M ≤ 10000
如：
100
输出描述
B能赢得比赛的组合次数
用例
| 输入 | 10 |
| 输出 | 1 |
| 说明 | 无 |
数学分析解法（可能会超时）
下面模拟M为10~14时，B能够获胜的一些情况：
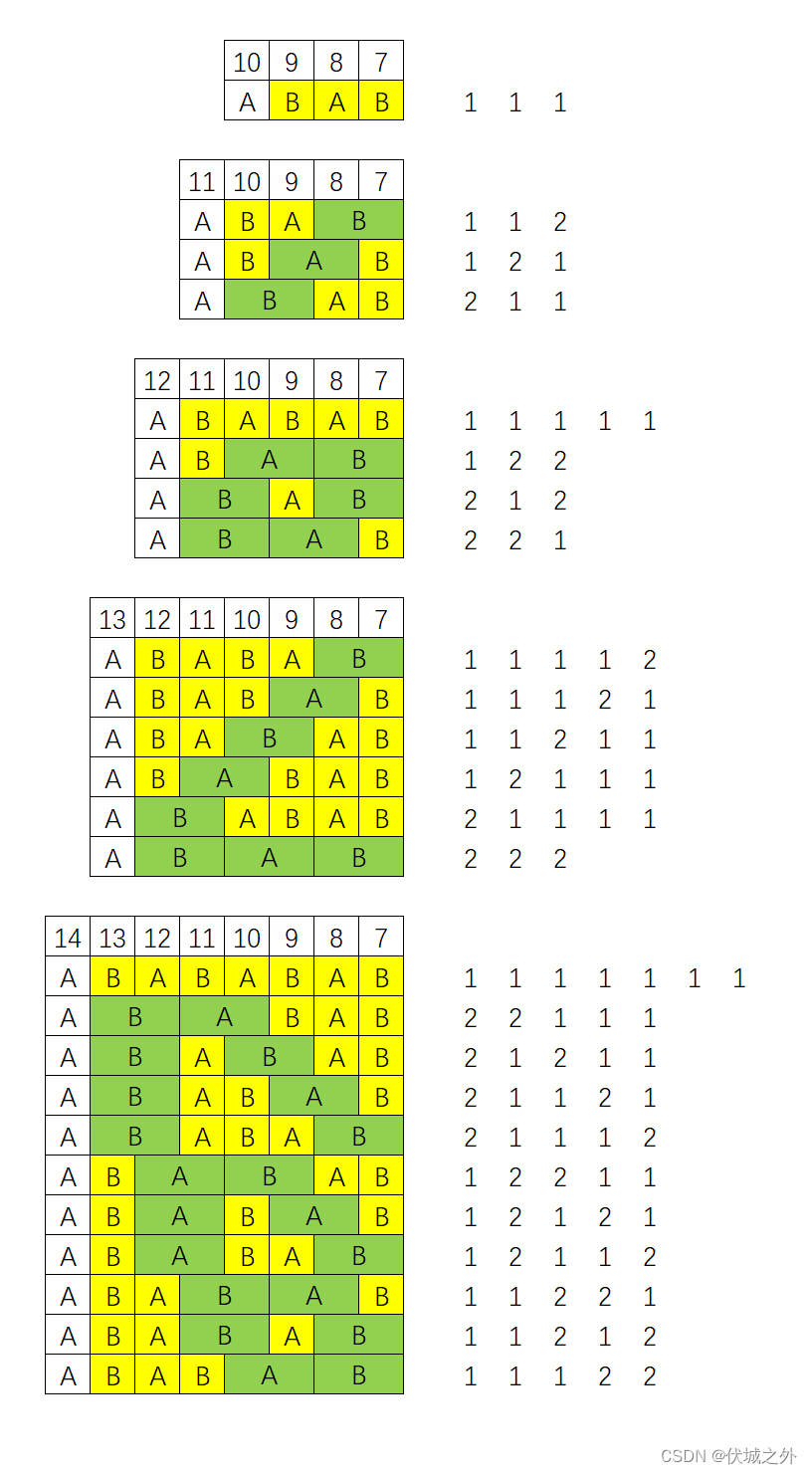
看完上图，我们可以发现：
抛开A首次叫的数字M，剩下的 M – 7 长度（上图中有颜色的），必须发生奇数次叫，才能保证B获胜。
原因是：奇数次叫中，第一次必然是B，由于是奇数次，因此最后一次也必然是B，比如
BAB
BABAB
都是奇数次。
因此我们只需要将整数 M – 7 划分为奇数块即可，且每块取值只能是1或2。
我们可以假设初始时，一共发生了M-7次叫（M-7可能不是奇数），即每块长度都是1，此时我们设
- oneCount = M – 7
- twoCount = 0
然后检查 oneCount + twoCount 的和（一共叫几次）：
- 若为奇数，则计算 oneCount 个 1 和 twoCount 个 2 形成的不重复的全排列的个数，统计进结果ans
- 若为偶数，则B无法获胜
之后，我们应该合并两个1为一个2，即：
- oneCount -= 2
- twoCount += 1
此时就会产生一种新的叫声情况，将新的oneCount和twoCount带入前面逻辑，进行循环处理，知道oneCount < 0 停止。
本题的数量级很大，10 ≤ M ≤ 10000，因此满足要求的情况数量可能极端大，此时我们应该使用大数记录结果。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const m = parseInt(await readline());
const factor = initFactor(m - 7);
let oneCount = m - 7;
let twoCount = 0;
// 记录B赢的情况数
let ans = BigInt(0);
while (oneCount >= 0) {
// 叫的次数为奇数时，才能B赢
if ((oneCount + twoCount) % 2 != 0) {
ans += getPermutationCount(oneCount, twoCount);
}
// 合并两个1为一个2
oneCount -= 2;
twoCount += 1;
}
console.log(ans.toString());
// 求解不重复的全排列数
function getPermutationCount(oneCount, twoCount) {
// 即 1 1 1 1 1 或 2 2 2 这种情况，此时只有一种排列
if (oneCount == 0 || twoCount == 0) {
return BigInt(1);
} else {
// 排列数去重，比如 1 1 1 2 2 的不重复排列数为 5! / 3! / 2! = 10
return factor[oneCount + twoCount] / factor[oneCount] / factor[twoCount];
}
}
// 阶乘
function initFactor(n) {
const factor = new Array(n + 1);
factor[0] = BigInt(1);
for (let i = 1; i <= n; i++) {
factor[i] = BigInt(i) * factor[i - 1];
}
return factor;
}
})();
Java算法源码
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
static BigInteger[] factor;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
initFactor(m - 7);
int oneCount = m - 7;
int twoCount = 0;
// 记录B赢的情况数
BigInteger ans = new BigInteger("0");
while (oneCount >= 0) {
// 叫的次数为奇数时，才能B赢
if ((oneCount + twoCount) % 2 != 0) {
ans = ans.add(getPermutationCount(oneCount, twoCount));
}
// 合并两个1为一个2
oneCount -= 2;
twoCount += 1;
}
System.out.println(ans);
}
// 求解不重复的全排列数
public static BigInteger getPermutationCount(int oneCount, int twoCount) {
if (oneCount == 0 || twoCount == 0) { // 即 1 1 1 1 1 或 2 2 2 这种情况，此时只有一种排列
return new BigInteger("1");
} else {
// 排列数去重，比如 1 1 1 2 2 的不重复排列数为 5! / 3! / 2! = 10
return factor[oneCount + twoCount].divide(factor[oneCount].multiply(factor[twoCount]));
}
}
// 阶乘
public static void initFactor(int n) {
factor = new BigInteger[n + 1];
factor[0] = new BigInteger("1");
for (int i = 1; i <= n; i++) {
factor[i] = factor[i - 1].multiply(new BigInteger(i + ""));
}
}
}
Python算法源码
这里Python进行了大数除法，因此数值类型变为了float，不在支持大数，所以需要使用decimal。
import decimal # 超大数运算内置库
from decimal import Decimal
decimal.setcontext(decimal.Context(prec=2500)) # 设置超大数精度
m = int(input())
factor = []
# 阶乘
def initFactor(n):
factor.append(Decimal(1))
for i in range(1, n+1):
factor.append(Decimal(i) * factor[-1])
# 求解不重复的全排列数
def getPermutationCount(oneCount, twoCount):
if oneCount == 0 or twoCount == 0:
# 即 1 1 1 1 1 或 2 2 2 这种情况，此时只有一种排列
return 1
else:
# 排列数去重，比如 1 1 1 2 2 的不重复排列数为 5! / 3! / 2! = 10
return factor[oneCount + twoCount] / factor[oneCount] / factor[twoCount]
def getResult():
initFactor(m - 7)
oneCount = m - 7
twoCount = 0
# 记录B赢的情况数
ans = Decimal(0)
while oneCount >= 0:
# 叫的次数为奇数时，才能B赢
if (oneCount + twoCount) % 2 != 0:
ans += getPermutationCount(oneCount, twoCount)
# 合并两个1为一个2
oneCount -= 2
twoCount += 1
return ans
print("{:.0f}".format(getResult()))
C算法源码
下面代码没有实现大数运算，关于大数运算可以参考：
#include <stdio.h>
// 阶乘
long long getFactor(int n) {
long long ans = 1;
for (int i = 2; i <= n; i++) {
ans *= i;
}
return ans;
}
// 求解不重复的全排列数
long long getPermutationCount(int oneCount, int twoCount) {
if (oneCount == 0 || twoCount == 0) {
// 即 1 1 1 1 1 或 2 2 2 这种情况，此时只有一种排列
return 1;
} else {
// 排列数去重，比如 1 1 1 2 2 的不重复排列数为 5! / 3! / 2! = 10
return getFactor(oneCount + twoCount) / getFactor(oneCount) / getFactor(twoCount);
}
}
int main() {
int m;
scanf("%d", &m);
int oneCount = m - 7;
int twoCount = 0;
// 记录B赢的情况数
long long ans = 0;
while (oneCount >= 0) {
// 叫的次数为奇数时，才能B赢
if ((oneCount + twoCount) % 2 != 0) {
ans += getPermutationCount(oneCount, twoCount);
}
// 合并两个1为一个2
oneCount -= 2;
twoCount += 1;
}
printf("%lld", ans);
return 0;
}动态规划解法（不会超时）
本题最优解法为动态规划，动态规划的逻辑很简单，假设A从m开始叫，那么：
B叫了数字 i 的方案数有多少种呢？
如果B叫了数字 i，那么上一把A可能会叫数字i+1，也可能叫数字i+2
dpB[i] 表示 B 能叫到数字 i 的方案数
dpA[i] 表示 A 能叫到数字 j 的方案数
那么 dpB[i] = dpA[i+1] + dpA[i+2]
同理的是，如果A叫了数字 i，那么上一把B可能会叫数字i+1，也可能会叫数字 i+2
那么 dpA[i] = dpB[i+1] + dpB[i+2]
初始时，是A从m开始叫，因此 dpA[m] = 1，即A叫到数字m的方案数为1。而B肯定叫不到数字m，因此初始化dpB[m] = 0。
之后我们可以递推出dpB[m-1]，即B叫出数字m-1的方案数，即dpB[m-1] = dpA[m] + dp[m+1]
提示，根据dpB[m-1] = dpA[m] + dpA[m+1]的递推式，我们可以了解到dpA,dpB数组的长度应该初始化为m+2，这样上面递推式才不会越界。
且dpA[m] = 1，dpA[m+1] = 0
而数字m-1，对于A而言是叫不到的，因此dpA[m-1]=0，但是也可以基于递推式得到：
dpA[m-1] = dpB[m] + dpB[m+1]，而dpB[m]和dpB[m+1]都应该初始化为0。
因此我们只需要按照上面递推式，一直递推到dpB[7]即可返回。
Java算法源码
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
// dpA[i] 表示 A 叫 数字i 的方案数
BigInteger[] dpA = new BigInteger[m + 2];
// 初始化dpA[i]
for (int i = 0; i < m + 2; i++) dpA[i] = new BigInteger("0");
// 由于是A从m开始叫，因此A叫m的方案数为1
dpA[m] = new BigInteger("1");
// dpB[i] 表示 B叫 数字i 的方案数
BigInteger[] dpB = new BigInteger[m + 2];
// 初始化dpB[i]
for (int i = 0; i < m + 2; i++) dpB[i] = new BigInteger("0");
for (int i = m - 1; i >= 7; i--) {
// B叫数字i的方案数 = A叫数字i+1的方案数 + A叫数字i+2的方案数
dpB[i] = dpA[i + 1].add(dpA[i + 2]);
// A叫数字i的方案数 = B叫数字i+1的方案数 + B叫数字i+2的方案数
dpA[i] = dpB[i + 1].add(dpB[i + 2]);
}
// 返回B叫7的方案数
System.out.println(dpB[7]);
}
}
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const m = parseInt(await readline());
// dpA[i] 表示 A 叫 数字i 的方案数
const dpA = new Array(m + 2).fill(0).map(() => BigInt(0));
// 由于是A从m开始叫，因此A叫m的方案数为1
dpA[m] = BigInt(1);
// dpB[i] 表示 B叫 数字i 的方案数
const dpB = new Array(m + 2).fill(0).map(() => BigInt(0));
for (let i = m - 1; i >= 7; i--) {
// B叫数字i的方案数 = A叫数字i+1的方案数 + A叫数字i+2的方案数
dpB[i] = dpA[i + 1] + dpA[i + 2];
// A叫数字i的方案数 = B叫数字i+1的方案数 + B叫数字i+2的方案数
dpA[i] = dpB[i + 1] + dpB[i + 2];
}
console.log(dpB[7].toString());
})();
Python算法源码
# 输入获取
m = int(input())
# 算法入口
def getResult():
# dpA[i] 表示 A 叫 数字i 的方案数
dpA = [0 for _ in range(m + 2)]
# 由于是A从m开始叫，因此A叫m的方案数为1
dpA[m] = 1
# dpB[i] 表示 B叫 数字i 的方案数
dpB = [0 for _ in range(m + 2)]
for i in range(m - 1, 6, -1):
# B叫数字i的方案数 = A叫数字i+1的方案数 + A叫数字i+2的方案数
dpB[i] = dpA[i + 1] + dpA[i + 2]
# A叫数字i的方案数 = B叫数字i+1的方案数 + B叫数字i+2的方案数
dpA[i] = dpB[i + 1] + dpB[i + 2]
# 返回B叫7的方案数
return dpB[7]
# 算法调用
print(getResult())C算法源码
下面代码没有实现大数运算，关于大数运算可以参考：
#include <stdio.h>
int main() {
int m;
scanf("%d", &m);
// dpA[i] 表示 A 叫 数字i 的方案数
long long dpA[m + 2];
// 初始化dpA[i]
for (int i = 0; i < m + 2; i++) dpA[i] = 0;
// 由于是A从m开始叫，因此A叫m的方案数为1
dpA[m] = 1;
// dpB[i] 表示 B叫 数字i 的方案数
long long dpB[m + 2];
// 初始化dpB[i]
for (int i = 0; i < m + 2; i++) dpB[i] = 0;
for (int i = m - 1; i >= 7; i--) {
// B叫数字i的方案数 = A叫数字i+1的方案数 + A叫数字i+2的方案数
dpB[i] = dpA[i + 1] + dpA[i + 2];
// A叫数字i的方案数 = B叫数字i+1的方案数 + B叫数字i+2的方案数
dpA[i] = dpB[i + 1] + dpB[i + 2];
}
// 返回B叫7的方案数
printf("%lld", dpB[7]);
return 0;
}免责声明：
1、IT资源小站为非营利性网站，全站所有资料仅供网友个人学习使用，禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享，本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题，请立即告知本站，本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体，但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员，一律视为同意网站规定，本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0