题目描述
推荐多样性需要从多个列表中选择元素,一次性要返回 N 屏数据(窗口数量),每屏展示 K 个元素(窗口大小),选择策略:
- 各个列表元素需要做穿插处理,即先从第一个列表中为每屏选择一个元素,再从第二个列表中为每屏选择一个元素,依次类推
- 每个列表的元素尽量均分为 N 份,如果不够 N 个,也要全部分配完,参考样例图:
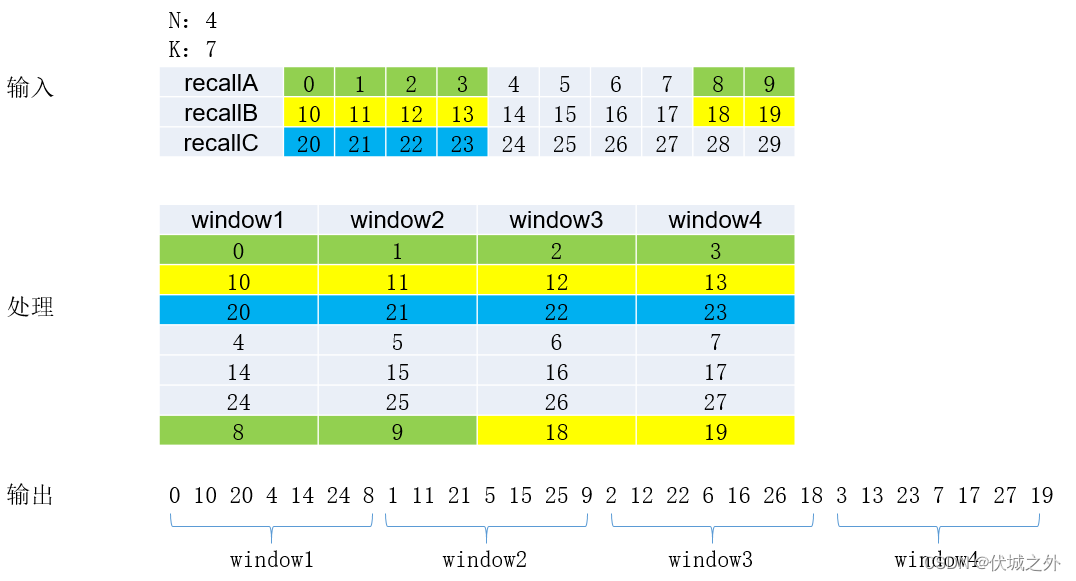
(1)从第一个列表中选择 4 条 0 1 2 3,分别放到 4 个窗口中
(2)从第二个列表中选择 4 条 10 11 12 13,分别放到 4 个窗口中
(3)从第三个列表中选择 4 条 20 21 22 23,分别放到 4 个窗口中
(4)再从第一个列表中选择 4 条 4 5 6 7,分别放到 4 个窗口中
…
(5)再从第一个列表中选择,由于数量不足 4 条,取剩下的 2 条,放到 窗口1 和 窗口2
(6)再从第二个列表中选择,由于数量不足 4 条并且总的元素数达到窗口要求,取 18 19 放到 窗口3 和 窗口4
输入描述
第一行输入为 N,表示需要输出的窗口数量,取值范围 [1, 10]
第二行输入为 K,表示每个窗口需要的元素数量,取值范围 [1, 100]
之后的行数不定(行数取值范围 [1, 10]),表示每个列表输出的元素列表。元素之间以空格隔开,已经过排序处理,每个列表输出的元素数量取值范围 [1, 100]
输出描述
输出元素列表,元素数量 = 窗口数量 * 窗口大小,元素之间以空格分隔,多个窗口合并为一个列表输出,参考样例:
先输出窗口1的元素列表,再输出窗口2的元素列表,再输出窗口3的元素列表,最后输出窗口4的元素列表
备注
- 每个列表会保证元素数量满足窗口要求,不需要考虑元素不足情况
- 每个列表的元素已去重,不需要考虑元素重复情况
- 每个列表的元素列表均不为空,不需要考虑列表为空的情况
- 每个列表的元素列表已经过排序处理,输出结果要保证不改变同一个列表的元素顺序
- 每个列表的元素数量可能是不同的
用例
| 输入 | 4 7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
| 输出 | 0 10 20 4 14 24 8 1 11 21 5 15 25 9 2 12 22 6 16 26 18 3 13 23 7 17 27 19 |
| 说明 | 无 |
题目解析
我们可以将最终的窗口集当成一个矩阵windows,该矩阵有 k 行 n 列,矩阵的每一列对应一个窗口。最终按列打印该矩阵,即为题解。
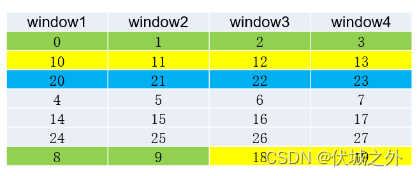
之后就是根据题目给定规则,往这个windos矩阵中填值即可。

由于填值过程是顺序的,即从左往右,从上往下地向windows矩阵中填值,因此我们可以将windows矩阵一维化,即定义为一维数组,数组长度为 k * n。
这样的话,只需要定义一个指针idx,就可以直到当前该往矩阵的哪个位置填值。
读取列表集的规则是:
从列表集的第一个列表开始读,每次读取n个值填到windows中,
- 如果当前列表的剩余元素个数 >= n,那么该列表读取完n个后,列表中还有剩余元素,即不需要像后面的列表借。
- 如果当前列表剩余元素个数 < n,那么该列表读取完后,还需要像后面的列表借。
需要注意的是,如果发生了“借”的动作,比如下面例子:
5
4
0 1 2 3 4
5 6 7 8
9 10 11 12 13 14
15 16 17 18 19
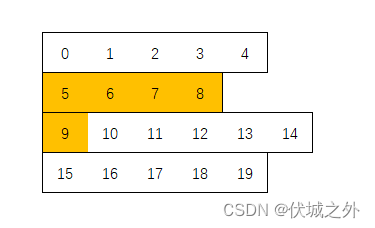
填充windows矩阵第二行时,由于第二个列表元素不足,因此"借"了第三个列表的元素,
那么下一轮填充windows矩阵第三行时,应该从列表集的第几个列表开始?
我理解应该是从第三个列表开始读,即最终读取出来的windows矩阵如下:

因此,在代码实现时,我们需要注意:
假设我们使用level指针指向当前轮次读取的列表的序号
- 当没有发生“借”动作时,当前列表读取完,我们需要level++
- 当发生了"借"动作时,由于当前列表元素不足,我们需要在读取过程中进行一次level++切到下一个列表借元素,当借完填到windows后,此时我们就不需要再次level++,因为当前已经处于了下一轮要读取的列表上。
2024.01.12
修复一个问题,即发生"借"动作时,即当前level列表的元素已用完,需要向下一个列表借,此时需要保证存在下一个列表,否则无法借。对应代码为:
JS:40行
Java:41行
Python:33行
C:111行
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const n = parseInt(await readline());
const k = parseInt(await readline());
const lists = [];
while (true) {
try {
const s = await readline();
if (s.length == 0) break;
lists.push(s.split(" ").map(Number));
} catch (e) {
break;
}
}
// 窗口矩阵,k行n列,每一列对应一个窗口,这里将二维矩阵一维化,方便后面赋值
const windows = new Array(k * n);
// 窗口矩阵中正在赋值的索引位置
let idx = 0;
// 正在从第level个列表中取值
let level = 0;
// 当窗口矩阵填满后,结束循环
while (idx < windows.length) {
// 当前轮次是否发生了"借"动作
let flag = false;
// 从第level个列表中取前n个元素
for (let i = 0; i < n; i++) {
windows[idx++] = lists[level].shift();
// 如果第level个列表没有元素了,则继续切到下一个列表中"借"
if (lists[level].length == 0 && lists.length > 1) {
lists.splice(level, 1); // 删除空列表
level %= lists.length; // 防止越界
flag = true; // 发生了"借"动作
}
}
// 如果没有发生"借"动作,则需要切到下一行
if (!flag) {
level = (level + 1) % lists.length; // 防止越界
}
}
const ans = [];
// 遍历列号
for (let j = 0; j < n; j++) {
// 遍历行号
for (let i = 0; i < k; i++) {
// 按列收集元素
ans.push(windows[i * n + j]);
}
}
console.log(ans.join(" "));
})();
Java算法源码
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());
int k = Integer.parseInt(sc.nextLine());
ArrayList<LinkedList<Integer>> lists = new ArrayList<>();
while (sc.hasNextLine()) {
String line = sc.nextLine();
// 本地测试,以空行作为输入截止条件
if (line.length() == 0) break;
Integer[] nums =
Arrays.stream(line.split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
lists.add(new LinkedList<>(Arrays.asList(nums)));
}
// 窗口矩阵,k行n列,每一列对应一个窗口,这里将二维矩阵一维化,方便后面赋值
int[] windows = new int[k * n];
// 窗口矩阵中正在赋值的索引位置
int idx = 0;
// 正在从第level个列表中取值
int level = 0;
// 当窗口矩阵填满后,结束循环
while (idx < windows.length) {
// 当前轮次是否发生了"借"动作
boolean flag = false;
// 从第level个列表中取前n个元素
for (int i = 0; i < n; i++) {
windows[idx++] = lists.get(level).removeFirst();
// 如果第level个列表没有元素了,则继续切到下一个列表中"借"
if (lists.get(level).size() == 0 && lists.size() > 1) {
lists.remove(level); // 删除空列表
level %= lists.size(); // 防止越界
flag = true; // 发生了"借"动作
}
}
// 如果没有发生"借"动作,则需要切到下一行
if (!flag) {
level = (level + 1) % lists.size(); // 防止越界
}
}
StringJoiner sj = new StringJoiner(" ");
// 遍历窗口矩阵的每一列
for (int j = 0; j < n; j++) { // 遍历列号
for (int i = 0; i < k; i++) { // 遍历行号
sj.add(windows[i * n + j] + ""); // 将每一列的元素进行拼接
}
}
System.out.println(sj);
}
}
Python算法源码
# 输入获取
n = int(input())
k = int(input())
lists = []
while True:
try:
lists.append(list(map(int, input().split())))
except:
break
# 算法入口
def getResult():
# 窗口矩阵,k行n列,每一列对应一个窗口,这里将二维矩阵一维化,方便后面赋值
windows = [0] * (k * n)
# 窗口矩阵中正在赋值的索引位置
idx = 0
# 正在从第level个列表中取值
level = 0
# 当窗口矩阵填满后,结束循环
while idx < len(windows):
# 当前轮次是否发生了"借"动作
flag = False
# 从第level个列表中取前n个元素
for _ in range(n):
windows[idx] = lists[level].pop(0)
idx += 1
# 如果第level个列表没有元素了,则继续切到下一个列表中"借"
if len(lists[level]) == 0 and len(lists) > 1:
lists.pop(level) # 删除空列表
level %= len(lists) # 防止越界
flag = True # 发生了"借"动作
# 如果没有发生"借"动作,则需要切到下一行
if not flag:
level = (level + 1) % len(lists) # 防止越界
ans = []
# 遍历列号
for j in range(n):
# 遍历行号
for i in range(k):
# 按列收集元素
ans.append(windows[i * n + j])
return " ".join(map(str, ans))
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MAX_ROWS 100
#define MAX_ROW_LEN 10000
/* 链表节点 */
typedef struct Node {
int val;
struct Node *next;
} Node;
/* 链表 */
typedef struct Link {
int size;
Node *head;
Node *tail;
} Link;
// 创建链表
Link *new_Link() {
Link *link = (Link *) malloc(sizeof(Link));
link->size = 0;
link->head = NULL;
link->tail = NULL;
return link;
}
// 尾插
void addLast_Link(Link *link, int val) {
Node *node = (Node *) malloc(sizeof(Node));
node->val = val;
node->next = NULL;
if (link->size == 0) {
link->head = node;
link->tail = node;
} else {
link->tail->next = node;
link->tail = node;
}
link->size++;
}
// 头删
int removeFirst_Link(Link *link) {
if (link->size == 0) exit(-1);
Node *removed = link->head;
if (link->size == 1) {
link->head = NULL;
link->tail = NULL;
} else {
link->head = link->head->next;
}
link->size--;
int val = removed->val;
free(removed);
return val;
}
int main() {
int n, k;
scanf("%d %d", &n, &k);
getchar();
Link *lists[MAX_ROWS];
int lists_size = 0;
char s[MAX_ROW_LEN];
while (gets(s)) {
// 本地测试,以空行作为输入截止条件
if (strlen(s) == 0) break;
Link *link = new_Link();
char *token = strtok(s, " ");
while (token != NULL) {
addLast_Link(link, atoi(token));
token = strtok(NULL, " ");
}
lists[lists_size++] = link;
}
// 窗口矩阵,k行n列,每一列对应一个窗口,这里将二维矩阵一维化,方便后面赋值
int windows[k * n];
// 窗口矩阵中正在赋值的索引位置
int idx = 0;
// 正在从第level个列表中取值
int level = 0;
// 当窗口矩阵填满后,结束循环
while (idx < k * n) {
// 当前轮次是否发生了"借"动作
int flag = 0;
// 从第level个列表中取前n个元素
for (int i = 0; i < n; i++) {
windows[idx++] = removeFirst_Link(lists[level]);
// 如果第level个列表没有元素了,则继续切到下一个列表中"借"
if (lists[level]->size == 0 && lists_size > 1) {
// 删除第level个空列表
for (int j = level + 1; j < lists_size; j++) {
lists[j - 1] = lists[j];
}
lists_size--;
level %= lists_size; // 防止越界
flag = 1; // 发生了"借"动作
}
}
// 如果没有发生"借"动作,则需要切到下一行
if (!flag) {
level = (level + 1) % lists_size; // 防止越界
}
}
// 遍历列号
for (int j = 0; j < n; j++) {
// 遍历行号
for (int i = 0; i < k; i++) {
// 按列打印
printf("%d", windows[i * n + j]);
if (j != n - 1 || i != k - 1) {
printf(" ");
}
}
}
return 0;
}免责声明:
评论0