题目描述
有一辆汽车需要从 m * n 的地图左上角(起点)开往地图的右下角(终点),去往每一个地区都需要消耗一定的油量,加油站可进行加油。
请你计算汽车确保从从起点到达终点时所需的最少初始油量。
说明:
- 智能汽车可以上下左右四个方向移动
- 地图上的数字取值是 0 或 -1 或 正整数:
-1 :表示加油站,可以加满油,汽车的油箱容量最大为100;
0 :表示这个地区是障碍物,汽车不能通过
正整数:表示汽车走过这个地区的耗油量
- 如果汽车无论如何都无法到达终点,则返回 -1
输入描述
第一行为两个数字,M,N,表示地图的大小为 M * N
- 0 < M,N ≤ 200
后面一个 M * N 的矩阵,其中的值是 0 或 -1 或正整数,加油站的总数不超过 200 个
输出描述
如果汽车无论如何都无法到达终点,则返回 -1
如果汽车可以到达终点,则返回最少的初始油量
用例
| 输入 | 2,2 10,20 30,40 |
| 输出 | 70 |
| 说明 | 行走的路线为:右→下 |
| 输入 | 4,4 10,30,30,20 30,30,-1,10 0,20,20,40 10,-1,30,40 |
| 输出 | 70 |
| 说明 | 行走的路线为:右→右→下→下→下→右 |
| 输入 | 4,5 10,0,30,-1,10 30,0,20,0,20 10,0,10,0,30 10,-1,30,0,10 |
| 输出 | 60 |
| 说明 | 行走的路线为:下→下→下→右→右→上→上→上→右→右→下→下→下 |
| 输入 | 4,4 10,30,30,20 30,30,20,10 10,20,10,40 10,20,30,40 |
| 输出 | -1 |
| 说明 | 无论如何都无法到达终点 |
题目解析
用例1路径
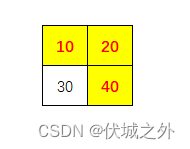
用例2路径
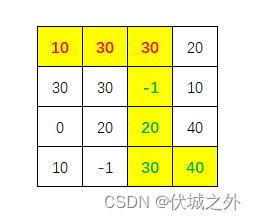
用例3路径
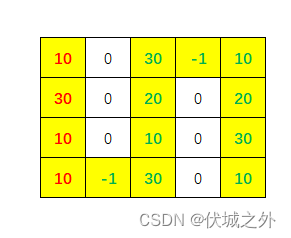
用例4:
由于汽车油箱容量最大100,因此即使初始时加满了油,也无法找到一条路径从起点到达终点
本题我有一个疑问,那就是否可以走回头路?我这里走回头路的目的是:尽可能地经过加油站,比如下面例子:
3,3
10,-1,40
30,0,50
50,-1,40
路线图如下,先走红色箭头路线,之后走绿色箭头
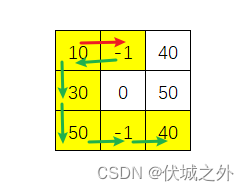
按照上面路线,初始只需要10个油即能完成从左上角开往右下角。
上面这种行驶路线我理解是可行的,也是符合本题要求的,同时也是符合实际生活场景的(车子快没油了,肯定是优先找一个就近的加油站先加油,即使加油站不在规划的路线上)。
本题的极限地图可以达到200*200,使用深搜DFS策略探路的话肯定会超时。
因此推荐使用广搜BFS策略探路。
当我们加起点加入到BFS队列后,此时即形成了一条路径,即起点(0,0)到(0,0)的路径,该路径的终点是(0,0),因此我们可以理解加入BFS队列中的位置点其实可以对应为某条路径的终点位置。
当我们从BFS队列弹出一个位置点A,其实就是选择某条路径,并从该路径的终点A,继续向其上下左右四个方向探路:
- 如果新位置B越界,则无法访问B
- 如果新位置B是障碍物,则无法访问B
除了上面两个判断外,我们还需要对A位置如下信息进行分析:
- 当前路径到达A点时,还剩余多少可用的油量,假设剩余可用油量为:A.remain
- 当前路径到达A点的过程中是否加过油?假设加油状态为:A.flag
- 当前路径到达A点所需的最少初始油量,假设最少初始油量为:A.init
如果新位置B本身是加油站的话,那么A->B的过程中:
- B.remain = 100 // 汽车到B位置后,会加满油
- B.init = A.init // 只需要 A.init 初始油量也可以到达B位置
- B.flag = true // 在B位置加油了
如果新位置B不是加油站的话,那么A->B的过程中:
- B.flag = A.flag // 加油状态沿用之前的
- B.remain = A.remain – matrix[B.x][B.y] // 汽车从A到B需要消耗matrix[B.x][B.y] 的油量,因此到B点后,剩余可用油量为 A.remain – matrix[B.x][B.y]
此时 B.remain 可能是负数,也可能不是负数:
- 如果 B.remain 是负数的话,则说明从 A 位置靠 A.remain 的剩余可用油量无法到B位置,此时有一个办法,那就是将这部分缺额油量计入到当前路径的初始油量中,即当前路径从起点出发时多带一点初始油量,且至少需要 A.init + (-B.remain) 初始油量,才能使得当前路径从起点到达B点,因此此时我们更新当前路径所需最少初始油量为 B.init = A.init + (-B.remain),注意此时B点为当前路径新的终点,因此当前路径的最少初始油量信息更新到B点上。同时注意更新 B.remain = 0。
- 如果 B.remain >= 0 的话,则说明从A位置可以靠 A.remain 的剩余可用油量到达B位置,所以B.init = A.init,即当前路径只需要A.init的初始油量,即可从起点到达B点。
注意:上面讨论 B.remain 是负数的时,表示当前路径到达B点还缺少(-B.remain)的油量,我们上面粗暴的将缺少的油量计入到了当前路径从起点出发时带的初始油量中,即初始油量多带(-B.remain)的油量,即可保证当前路径刚刚好到达B点时消耗完所有的油。
但是,上面这个粗暴计入是存在问题的,请看下图:
(0, 0) -> (0, 0) 至少需要初始油量10,如果初始油量10,那么此时剩余可用0
(0, 0) -> (1, 0) 至少需要初始油量40,如果初始油量40,那么此时剩余可用0
(0, 0) -> (1, 0) -> (2, 0) 至少需要初始油量40,此时加满了油,剩余可用100
(0, 0) -> (1, 0) -> (2, 0) -> (2, 1) 至少需要初始油量40,剩余可用30
(0, 0) -> (1, 0) -> (2, 0) -> (2, 1) -> (2, 2) 由于上一步剩余可用只有30,而到达终点(2,2)需要40的油量,还缺10个油,那么这里缺的10个油,能粗暴的计入到初始油量里面吗?
假设我们粗暴的计入到初始油量中,即当前路径从起点出发时初始油量50个,那么
(0, 0) -> (0, 0),剩余可用40
(0, 0) -> (1, 0),剩余可用10
(0, 0) -> (1, 0) -> (2, 0),加满了油,剩余可用100
(0, 0) -> (1, 0) -> (2, 0) -> (2, 1) ,剩余可用30
(0, 0) -> (1, 0) -> (2, 0) -> (2, 1) -> (2, 2) ,此时上一步剩余油量还是不够????为啥?
问题出在,该路径到达(2,2)前加过一次油了,因此该路径是从某个位置以满油状态来的,因此即使你给初始油量加再多,中间过程必然会变一次满油状态,而满油状态也无法到达(2,2),因此该路径无法到达(2,2)。
总结一下就是,如果A->B过程中,油量不够了,此时我们期望是将缺额油量计入到初始油量中,但是到达B之前的过程中不能加过油,否则此时缺额的油无法通过初始油量补充得到。
还有一个问题,如果上面A->B缺少的油,可以计入到当前路径的初始油量中,那么如果是下面例子,还可以借吗?
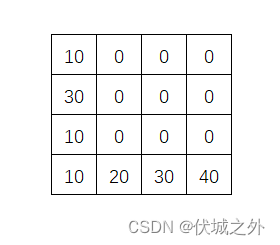
即我们每走一步都将缺少油计入到初始油量中,但是汽车油箱只有100个单位,如果缺少的油超过了100个单位,那么对应路径也不大可达终点。
最后一个问题:本题允许回路,那么如何避免因为回路产生的死循环?
其实处理办法很简单,我们可以定义一个矩阵dist_init,其中元素dist_init[x][y] 用于记录起点到(x,y)的所有路径中的最优路径(即需要最少初始油量的路径)的初始油量。
每当我们BFS探索过(弹出)一个点(x,y)后,我们就得到了一条路径到达(x,y)点的最少初始油量init,我们比较 init 和 dist_init[x][y],
- 如果 init < dist_init[x][y],则说明当前路径到达(x,y)更优,花费更少的初始油量 init,此时我们更新 dist_init[x][y] = init
- 如果 init > dist_init[x][y],则说明当前路径到达(x,y)不是最优的,因此当前路径也没必要继续往后探索了,可以终止当前路径的探索。
而回路是指(x1,y1) -> (x2, y2) -> (x1, y1),如果 (x2, y2)不是加油站,那么此时(x2, y2) -> (x1, y1)的探路对应的init,对于(x1, y1)而言必然不是最优的,按照上面逻辑,可以终止该回路,避免死循环。比如下图:
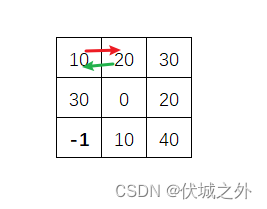
(0, 0) -> (0, 1) -> (0, 0) ,该路径到达(0,0) 所需的最少初始油量为 40
(0, 0) -> (0, 0),该路径到达(0,0) 所需的最少初始油量为 10
因此终止回路(0, 0) -> (0, 1) -> (0, 0)的后续探索
但是如果回路过程中遇到加油站,比如下图:
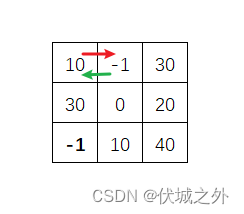
- (0, 0) -> (0, 1) -> (0, 0) ,该路径到达(0,0) 所需的最少初始油量为 10
- (0, 0) -> (0, 0),该路径到达(0,0) 所需的最少初始油量为 10
此时两个路径的初始油量都只需要10,那么我们应该选择哪一种路径呢?
对于初始油量相同的,我们应该关注剩余可用油量更多的,比如上图:
- (0, 0) -> (0, 1) -> (0, 0) ,该路径到达(0,0) 时,剩余可用油量为90
- (0, 0) -> (0, 0),该路径到达(0,0) 时,剩余可用油量为0
此时我们选择剩余油量更多的路径更优。即此时回路更优。
因此,我们还需要定义一个矩阵 dist_remain , 其中元素dist_remain [x][y] 用于记录起点到(x,y)的所有路径中的最优路径(即需要最少初始油量的路径,如果由多条路径的最少初始油量相同,则选择这些路径中剩余油量更多的)的剩余可用油量。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const [m, n] = (await readline()).split(",").map(Number);
const matrix = [];
for (let i = 0; i < m; i++) {
matrix.push((await readline()).split(",").map(Number));
}
// 上下左右四个方向对应的偏移量
const offsets = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1],
];
// 记录路径中位置的几个状态
class Node {
constructor(x, y) {
this.x = x; // 位置横坐标
this.y = y; // 位置纵坐标
this.init = 0; // 到达此位置所需的最少初始油量
this.remain = 0; // 到达此位置时剩余可用油量
this.flag = false; // 到达此位置前有没有加过油
}
}
function bfs() {
// 如果左上角和右下角不可达,则直接返回-1
if (matrix[0][0] == 0 || matrix[m - 1][n - 1] == 0) {
return -1;
}
// 广搜队列
const queue = [];
// 起始位置
const src = new Node(0, 0);
if (matrix[0][0] == -1) {
// 如果起始位置就是加油站,则到达(0,0)位置所需初始油量为0,且剩余可用油量为100,且需要标记已加油
src.init = 0;
src.remain = 100;
src.flag = true;
} else {
// 如果起始位置不是加油站,则到达(0,0)位置所需的初始油量至少为matrix[0][0], 剩余可用油量为0,未加油状态
src.init = matrix[0][0];
src.remain = 0;
src.flag = false;
}
queue.push(src);
// dist_init[x][y] 用于记录起点 (0, 0) 到达 (x, y) 的所有可达路径中最优路径(即初始油量需求最少的路径)的初始油量
const dist_init = new Array(m)
.fill(0)
.map(() => new Array(n).fill(Infinity)); // 由于需要记录每个位置的最少需要的初始油量,因此每个位置所需的初始油量初始化为一个较大值
// dist_remain 用于记录起点 (0,0) 到达 (x,y) 的所有可达路径中最优路径(即初始油量需求最少的路径)的最大剩余可用油量
// 即如果存在多条最优路径,我们应该选这些路径中到达此位置剩余油量最多的
const dist_remain = new Array(m).fill(0).map(() => new Array(n).fill(0));
// 起点(0,0)到达自身位置(0,0)所需的最少初始油量和最多剩余油量
dist_init[0][0] = src.init;
dist_remain[0][0] = src.remain;
// 广搜
while (queue.length > 0) {
const cur = queue.shift();
// 从当前位置cur开始向上下左右四个方向探路
for (let [offsetX, offsetY] of offsets) {
// 新位置
const newX = cur.x + offsetX;
const newY = cur.y + offsetY;
// 新位置越界 或者 新位置是障碍,则新位置不可达,继续探索其他方向
if (
newX < 0 ||
newX >= m ||
newY < 0 ||
newY >= n ||
matrix[newX][newY] == 0
) {
continue;
}
// 如果新位置可达,则计算到达新位置的三个状态数据
let init = cur.init; // 到达新位置所需的最少初始油量
let remain = cur.remain; // 到达新位置时还剩余的最多可用油量
let flag = cur.flag; // 是否加油了
if (matrix[newX][newY] == -1) {
// 如果新位置是加油站,则加满油
remain = 100;
// 标记加过油了
flag = true;
} else {
// 如果新位置不是加油站,则需要消耗matrix[newX][newY]个油
remain -= matrix[newX][newY];
}
// 如果到达新位置后,剩余油量为负数
if (remain < 0) {
if (flag) {
// 如果之前已经加过油了,则说明到达此路径前是满油状态,因此我们无法从初始油量里面"借"油
continue;
} else {
// 如果之前没有加过油,则超出的油量(-remain),可以从初始油量里面"借",即需要初始油量 init + (-remain) 才能到达新位置
init -= remain;
// 由于初始油量 init + (-remain) 刚好只能支持汽车到达新位置,因此汽车到达新位置后剩余可用油量为0
remain = 0;
}
}
// 如果到达新位置所需的初始油量超过了满油100,则无法到达新位置
if (init > 100) {
continue;
}
// 如果可达新位置,则继续检查当前路径策略到达新位置(newX, newY)所需的初始油量init是否比其他路径策略更少
if (init > dist_init[newX][newY]) {
// 如果不是,则无需探索新位置(newX, newY)
continue;
}
// 当前路径策略到达新位置(newX,newY)所需初始油量init更少,或者,init和前面路径策略相同,但是当前路径策略剩余可用油量remain更多
if (init < dist_init[newX][newY] || remain > dist_remain[newX][newY]) {
// 则当前路径策略更优,记录更优路径的状态
dist_init[newX][newY] = init;
dist_remain[newX][newY] = remain;
// 将当前新位置加入BFS队列
const next = new Node(newX, newY);
next.init = init;
next.remain = remain;
next.flag = flag;
queue.push(next);
}
}
}
// dist_init[m - 1][n - 1] 记录的是到达右下角终点位置所需的最少初始油量
return dist_init[m - 1][n - 1] == Infinity ? -1 : dist_init[m - 1][n - 1];
}
console.log(bfs());
})();
Java算法源码
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
static int m;
static int n;
static int[][] matrix;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in).useDelimiter("[,n]"); // 将逗号和换行符作为一次读取的截止符
m = sc.nextInt();
n = sc.nextInt();
matrix = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j] = sc.nextInt();
}
}
System.out.println(bfs());
}
// 上下左右四个方向对应的偏移量
static int[][] offsets = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
// 记录路径中位置的几个状态
static class Node {
int x; // 位置横坐标
int y; // 位置纵坐标
int init; // 到达此位置所需的最少初始油量
int remain; // 到达此位置时剩余可用油量
boolean flag; // 到达此位置前有没有加过油
public Node(int x, int y) {
this.x = x;
this.y = y;
}
}
public static int bfs() {
// 如果左上角和右下角不可达,则直接返回-1
if (matrix[0][0] == 0 || matrix[m - 1][n - 1] == 0) {
return -1;
}
// 广搜队列
LinkedList<Node> queue = new LinkedList<>();
// 起始位置
Node src = new Node(0, 0);
if (matrix[0][0] == -1) {
// 如果起始位置就是加油站,则到达(0,0)位置所需初始油量为0,且剩余可用油量为100,且需要标记已加油
src.init = 0;
src.remain = 100;
src.flag = true;
} else {
// 如果起始位置不是加油站,则到达(0,0)位置所需的初始油量至少为matrix[0][0], 剩余可用油量为0,未加油状态
src.init = matrix[0][0];
src.remain = 0;
src.flag = false;
}
queue.add(src);
// dist_init[x][y] 用于记录起点 (0, 0) 到达 (x, y) 的所有可达路径中最优路径(即初始油量需求最少的路径)的初始油量
int[][] dist_init = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 由于需要记录每个位置的最少需要的初始油量,因此每个位置所需的初始油量初始化为一个较大值
dist_init[i][j] = Integer.MAX_VALUE;
}
}
// dist_remain 用于记录起点 (0,0) 到达 (x,y) 的所有可达路径中最优路径(即初始油量需求最少的路径)的最大剩余可用油量
// 即如果存在多条最优路径,我们应该选这些路径中到达此位置剩余油量最多的
int[][] dist_remain = new int[m][n];
// 起点(0,0)到达自身位置(0,0)所需的最少初始油量和最多剩余油量
dist_init[0][0] = src.init;
dist_remain[0][0] = src.remain;
// 广搜
while (queue.size() > 0) {
Node cur = queue.removeFirst();
// 从当前位置cur开始向上下左右四个方向探路
for (int[] offset : offsets) {
// 新位置
int newX = cur.x + offset[0];
int newY = cur.y + offset[1];
// 新位置越界 或者 新位置是障碍,则新位置不可达,继续探索其他方向
if (newX < 0 || newX >= m || newY < 0 || newY >= n || matrix[newX][newY] == 0) continue;
// 如果新位置可达,则计算到达新位置的三个状态数据
int init = cur.init; // 到达新位置所需的最少初始油量
int remain = cur.remain; // 到达新位置时还剩余的最多可用油量
boolean flag = cur.flag; // 是否加油了
if (matrix[newX][newY] == -1) {
// 如果新位置是加油站,则加满油
remain = 100;
// 标记加过油了
flag = true;
} else {
// 如果新位置不是加油站,则需要消耗matrix[newX][newY]个油
remain -= matrix[newX][newY];
}
// 如果到达新位置后,剩余油量为负数
if (remain < 0) {
if (flag) {
// 如果之前已经加过油了,则说明到达此路径前是满油状态,因此我们无法从初始油量里面"借"油
continue;
} else {
// 如果之前没有加过油,则超出的油量(-remain),可以从初始油量里面"借",即需要初始油量 init + (-remain) 才能到达新位置
init -= remain;
// 由于初始油量 init + (-remain) 刚好只能支持汽车到达新位置,因此汽车到达新位置后剩余可用油量为0
remain = 0;
}
}
// 如果到达新位置所需的初始油量超过了满油100,则无法到达新位置
if (init > 100) {
continue;
}
// 如果可达新位置,则继续检查当前路径策略到达新位置(newX, newY)所需的初始油量init是否比其他路径策略更少
if (init > dist_init[newX][newY]) {
// 如果不是,则无需探索新位置(newX, newY)
continue;
}
// 当前路径策略到达新位置(newX,newY)所需初始油量init更少,或者,init和前面路径策略相同,但是当前路径策略剩余可用油量remain更多
if (init < dist_init[newX][newY] || remain > dist_remain[newX][newY]) {
// 则当前路径策略更优,记录更优路径的状态
dist_init[newX][newY] = init;
dist_remain[newX][newY] = remain;
// 将当前新位置加入BFS队列
Node next = new Node(newX, newY);
next.init = init;
next.remain = remain;
next.flag = flag;
queue.add(next);
}
}
}
// dist_init[m - 1][n - 1] 记录的是到达右下角终点位置所需的最少初始油量
return dist_init[m - 1][n - 1] == Integer.MAX_VALUE ? -1 : dist_init[m - 1][n - 1];
}
}
Python算法源码
import sys
# 输入获取
m, n = map(int, input().split(","))
matrix = [list(map(int, input().split(","))) for _ in range(m)]
# 上下左右四个方向对应的偏移量
offsets = ((-1, 0), (1, 0), (0, -1), (0, 1))
# 记录路径中位置的几个状态
class Node:
def __init__(self, x, y):
self.x = x # 位置横坐标
self.y = y # 位置纵坐标
self.init = 0 # 到达此位置所需的最少初始油量
self.remain = 0 # 到达此位置时剩余可用油量
self.flag = False # 到达此位置前有没有加过油
# 算法入口
def bfs():
# 如果左上角和右下角不可达,则直接返回-1
if matrix[0][0] == 0 or matrix[m - 1][n - 1] == 0:
return -1
# 广搜队列
queue = []
# 起始位置
src = Node(0, 0)
if matrix[0][0] == -1:
# 如果起始位置就是加油站,则到达(0,0)位置所需初始油量为0,且剩余可用油量为100,且需要标记已加油
src.init = 0
src.remain = 100
src.flag = True
else:
# 如果起始位置不是加油站,则到达(0,0)位置所需的初始油量至少为matrix[0][0], 剩余可用油量为0,未加油状态
src.init = matrix[0][0]
src.remain = 0
src.flag = False
queue.append(src)
# dist_init[x][y] 用于记录起点 (0, 0) 到达 (x, y) 的所有可达路径中最优路径(即初始油量需求最少的路径)的初始油量
# 由于需要记录每个位置的最少需要的初始油量,因此每个位置所需的初始油量初始化为一个较大值
dist_init = [[sys.maxsize] * n for _ in range(m)]
# dist_remain 用于记录起点 (0,0) 到达 (x,y) 的所有可达路径中最优路径(即初始油量需求最少的路径)的最大剩余可用油量
# 即如果存在多条最优路径,我们应该选这些路径中到达此位置剩余油量最多的
dist_remain = [[0] * n for _ in range(m)]
# 起点(0,0)到达自身位置(0,0)所需的最少初始油量和最多剩余油量
dist_init[0][0] = src.init
dist_remain[0][0] = src.remain
# 广搜
while len(queue) > 0:
cur = queue.pop(0)
# 从当前位置cur开始向上下左右四个方向探路
for offsetX, offsetY in offsets:
# 新位置
newX = cur.x + offsetX
newY = cur.y + offsetY
# 新位置越界 或者 新位置是障碍,则新位置不可达,继续探索其他方向
if newX < 0 or newX >= m or newY < 0 or newY >= n or matrix[newX][newY] == 0:
continue
# 如果新位置可达,则计算到达新位置的三个状态数据
init = cur.init # 到达新位置所需的最少初始油量
remain = cur.remain # 到达新位置时还剩余的最多可用油量
flag = cur.flag # 是否加油了
if matrix[newX][newY] == -1:
# 如果新位置是加油站,则加满油
remain = 100
# 标记加过油了
flag = True
else:
# 如果新位置不是加油站,则需要消耗matrix[newX][newY]个油
remain -= matrix[newX][newY]
# 如果到达新位置后,剩余油量为负数
if remain < 0:
if flag:
# 如果之前已经加过油了,则说明到达此路径前是满油状态,因此我们无法从初始油量里面"借"油
continue
else:
# 如果之前没有加过油,则超出的油量(-remain),可以从初始油量里面"借",即需要初始油量 init + (-remain) 才能到达新位置
init -= remain
# 由于初始油量 init + (-remain) 刚好只能支持汽车到达新位置,因此汽车到达新位置后剩余可用油量为0
remain = 0
# 如果到达新位置所需的初始油量超过了满油100,则无法到达新位置
if init > 100:
continue
# 如果可达新位置,则继续检查当前路径策略到达新位置(newX, newY)所需的初始油量init是否比其他路径策略更少
if init > dist_init[newX][newY]:
# 如果不是,则无需探索新位置(newX, newY)
continue
# 当前路径策略到达新位置(newX,newY)所需初始油量init更少,或者,init和前面路径策略相同,但是当前路径策略剩余可用油量remain更多
if init < dist_init[newX][newY] or remain > dist_remain[newX][newY]:
# 则当前路径策略更优,记录更优路径的状态
dist_init[newX][newY] = init
dist_remain[newX][newY] = remain
# 将当前新位置加入BFS队列
nxt = Node(newX, newY)
nxt.init = init
nxt.remain = remain
nxt.flag = flag
queue.append(nxt)
# dist_init[m - 1][n - 1] 记录的是到达右下角终点位置所需的最少初始油量
if dist_init[m - 1][n - 1] == sys.maxsize:
return -1
else:
return dist_init[m - 1][n - 1]
# 算法调用
print(bfs())
C算法源码
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define MAX_SIZE 200
// 记录路径中位置的几个状态
typedef struct {
int x; // 位置横坐标
int y; // 位置纵坐标
int init; // 到达此位置所需的最少初始油量
int remain; // 到达此位置时剩余可用油量
int flag; // 到达此位置前有没有加过油
} Node;
Node *new_Node(int x, int y) {
Node *node = (Node *) malloc(sizeof(Node));
node->x = x;
node->y = y;
node->init = 0;
node->remain = 0;
node->flag = 0;
return node;
}
/** 基于链表实现队列 **/
typedef struct ListNode {
Node *ele;
struct ListNode *next;
} ListNode;
typedef struct LinkedList {
int size;
ListNode *head;
ListNode *tail;
} LinkedList;
LinkedList *new_LinkedList() {
LinkedList *link = (LinkedList *) malloc(sizeof(LinkedList));
link->size = 0;
link->head = NULL;
link->tail = NULL;
return link;
}
void addLast_LinkedList(LinkedList *link, Node *ele) {
ListNode *node = (ListNode *) malloc(sizeof(ListNode));
node->ele = ele;
node->next = NULL;
if (link->size == 0) {
link->head = node;
link->tail = node;
} else {
link->tail->next = node;
link->tail = node;
}
link->size++;
}
Node *removeFirst_LinkedList(LinkedList *link) {
if (link->size == 0) exit(-1);
ListNode *removed = link->head;
if (link->size == 1) {
link->head = NULL;
link->tail = NULL;
} else {
link->head = link->head->next;
}
link->size--;
return removed->ele;
}
// m * n 的地图
int m, n;
// 地图矩阵
int matrix[MAX_SIZE][MAX_SIZE];
// 上下左右四个方向对应的偏移量
int offsets[4][2] = {{-1, 0},
{1, 0},
{0, -1},
{0, 1}};
int bfs() {
// 如果左上角和右下角不可达,则直接返回-1
if (matrix[0][0] == 0 || matrix[m - 1][n - 1] == 0) {
return -1;
}
// 广搜队列
LinkedList *queue = new_LinkedList();
// 起始位置
Node *src = new_Node(0, 0);
if (matrix[0][0] == -1) {
// 如果起始位置就是加油站,则到达(0,0)位置所需初始油量为0,且剩余可用油量为100,且需要标记已加油
src->init = 0;
src->remain = 100;
src->flag = 1;
} else {
// 如果起始位置不是加油站,则到达(0,0)位置所需的初始油量至少为matrix[0][0], 剩余可用油量为0,未加油状态
src->init = matrix[0][0];
src->remain = 0;
src->flag = 0;
}
addLast_LinkedList(queue, src);
// dist_init[x][y] 用于记录起点 (0, 0) 到达 (x, y) 的所有可达路径中最优路径(即初始油量需求最少的路径)的初始油量
int dist_init[MAX_SIZE][MAX_SIZE];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 由于需要记录每个位置的最少需要的初始油量,因此每个位置所需的初始油量初始化为一个较大值
dist_init[i][j] = INT_MAX;
}
}
// dist_remain 用于记录起点 (0,0) 到达 (x,y) 的所有可达路径中最优路径(即初始油量需求最少的路径)的最大剩余可用油量
// 即如果存在多条最优路径,我们应该选这些路径中到达此位置剩余油量最多的
int dist_remain[MAX_SIZE][MAX_SIZE] = {0};
// 起点(0,0)到达自身位置(0,0)所需的最少初始油量和最多剩余油量
dist_init[0][0] = src->init;
dist_remain[0][0] = src->remain;
// 广搜
while (queue->size > 0) {
Node *cur = removeFirst_LinkedList(queue);
// 从当前位置cur开始向上下左右四个方向探路
for (int i = 0; i < 4; i++) {
// 新位置
int newX = cur->x + offsets[i][0];
int newY = cur->y + offsets[i][1];
// 新位置越界 或者 新位置是障碍,则新位置不可达,继续探索其他方向
if (newX < 0 || newX >= m || newY < 0 || newY >= n || matrix[newX][newY] == 0) {
continue;
}
// 如果新位置可达,则计算到达新位置的三个状态数据
int init = cur->init; // 到达新位置所需的最少初始油量
int remain = cur->remain; // 到达新位置时还剩余的最多可用油量
int flag = cur->flag; // 是否加油了
if (matrix[newX][newY] == -1) {
// 如果新位置是加油站,则加满油
remain = 100;
// 标记加过油了
flag = 1;
} else {
// 如果新位置不是加油站,则需要消耗matrix[newX][newY]个油
remain -= matrix[newX][newY];
}
// 如果到达新位置后,剩余油量为负数
if (remain < 0) {
if (flag) {
// 如果之前已经加过油了,则说明到达此路径前是满油状态,因此我们无法从初始油量里面"借"油
continue;
} else {
// 如果之前没有加过油,则超出的油量(-remain),可以从初始油量里面"借",即需要初始油量 init + (-remain) 才能到达新位置
init -= remain;
// 由于初始油量 init + (-remain) 刚好只能支持汽车到达新位置,因此汽车到达新位置后剩余可用油量为0
remain = 0;
}
}
// 如果到达新位置所需的初始油量超过了满油100,则无法到达新位置
if (init > 100) {
continue;
}
// 如果可达新位置,则继续检查当前路径策略到达新位置(newX, newY)所需的初始油量init是否比其他路径策略更少
if (init > dist_init[newX][newY]) {
// 如果不是,则无需探索新位置(newX, newY)
continue;
}
// 当前路径策略到达新位置(newX,newY)所需初始油量init更少,或者,init和前面路径策略相同,但是当前路径策略剩余可用油量remain更多
if (init < dist_init[newX][newY] || remain > dist_remain[newX][newY]) {
// 则当前路径策略更优,记录更优路径的状态
dist_init[newX][newY] = init;
dist_remain[newX][newY] = remain;
// 将当前新位置加入BFS队列
Node *next = new_Node(newX, newY);
next->init = init;
next->remain = remain;
next->flag = flag;
addLast_LinkedList(queue, next);
}
}
}
// dist_init[m - 1][n - 1] 记录的是到达右下角终点位置所需的最少初始油量
if (dist_init[m - 1][n - 1] == INT_MAX) {
return -1;
} else {
return dist_init[m - 1][n - 1];
}
}
int main() {
scanf("%d,%d", &m, &n);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &matrix[i][j]);
getchar();
}
}
printf("%dn", bfs());
return 0;
}免责声明:
评论0