题目描述
疫情期间需要大家保证一定的社交距离,公司组织开交流会议。
座位一排共 N 个座位,编号分别为 [0, N – 1] 。
要求员工一个接着一个进入会议室,并且可以在任何时候离开会议室。
满足:
- 每当一个员工进入时,需要坐到最大社交距离(最大化自己和其他人的距离的座位);
- 如果有多个这样的座位,则坐到索引最小的那个座位。
输入描述
会议室座位总数 seatNum
- 1 ≤ seatNum ≤ 500
员工的进出顺序 seatOrLeave 数组
- 元素值为 1,表示进场
- 元素值为负数,表示出场(特殊:位置 0 的员工不会离开)
例如 -4 表示坐在位置 4 的员工离开(保证有员工坐在该座位上)
输出描述
最后进来员工,他会坐在第几个位置,如果位置已满,则输出-1。
用例
| 输入 | 10 [1, 1, 1, 1, -4, 1] |
| 输出 | 5 |
| 说明 |
seat -> 0,空在任何位置都行,但是要给他安排索引最小的位置,也就是座位 0 seat -> 9,要和旁边的人距离最远,也就是座位 9 seat -> 4,要和旁边的人距离最远,应该坐到中间,也就是座位 4 seat -> 2,员工最后坐在 2 号座位上 leave[4], 4 号座位的员工离开 seat -> 5,员工最后坐在 5 号座位上 |
题目解析
我的解题思路如下:
首先,定义一个集合 seatIdx 用于记录已经坐人的座位号。
然后,遍历第二行输入的员工出入顺序数组,如果遍历出来的数组元素info:
- info值为负数,则坐在 -info 座位号的员工要离开,我们应该将 -info 从 seatIdx 中去除。
- info值为正数,则有一个员工要进来入座,我们需要找到具有最大社交距离的座位给这个员工:
假设座位使用情况如:[1, 0, 0, 1, 0 , 0, 0],其中1代表有人坐,0代表没人坐。
我们观察其中的连续空闲座位情况,连续空闲座位的左右边界有如下情况:
1、左右边界都无人,此时必然是所有座位都为空:[0, 0, 0, 0, 0],因为题目说:位置 0 的员工不会离开
2、左右边界都有人:[1, 0, 0, 1, 0 , 0, 0]
3、左边界有人,右边界无人:[1, 0, 0, 1, 0 , 0, 0]
4、左边界无人,右边界有人,本题不存在这种情况,因为题目说:位置 0 的员工不会离开
如果有员工要入座,则检查:
如果seatIdx.size == 0,则说明所有座位都是空的,此时对应员工直接做到第0个座位
如果seatIdx.size == 1,则说明只有一个座位坐了人,那么该座位肯定是第0个座位,因此当前要入座的员工,最大社交距离位置是第 seatNum – 1 个位置
如果seatIdx.size > 1,则此时我们需要遍历seatIdx,即遍历出哪些座位做了人?一次遍历两个,即获得了连续空闲座位的左右边界,假设左边界是left,右边界是right,
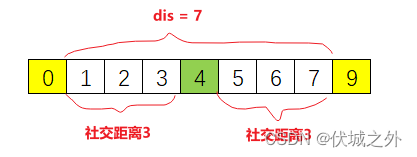
那么连续空闲座位长度 dis = right – left – 1,如下图所示:
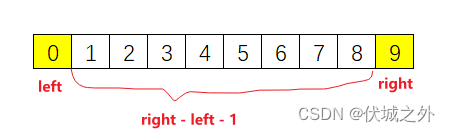
此时该连续空闲座位中选一个具有最大社交距离的位置,通过图示,我们可以很容易判断出是第4个位置。
求解时,我们可以先根据dist求出最大社交距离curSeatDis为:
curSeatDis = dis / 2
如果 dis 是偶数,则还需要: curSeatDis -= 1,比如下图dis = 8,座位4的社交距离 = 8 / 2 – 1 = 3
如果 dis 是奇数,则不需要做处理,比如下图:
得到当前空闲区域的最大社交距离后,我们即可求出当前空闲区域具备最大社交距离的座位号:
curSeatIdx = left + curSeatDis + 1
如果当前座位情况存在多个连续空闲座位区域,比如 [1, 0, 0, 0, 1, 0, 0, 1, 0 , 0 , 0, 0 , 1]
此时,我们应该按照上面逻辑,求出每一个空闲区域的最大社交距离,如果对应空闲区域的最大社交距离更大,则对应空闲区域可以得到更优的座位。
题目说:
如果有多个这样的座位,则坐到索引最小的那个座位。
因此,只有当前空闲区域的最大社交距离严格大于前面的,才能更新最优座位号。这样可以保证出现相同最大社交距离时,可以保留索引较小的座位号。
另外,还有一种特殊情况,比如下面座位使用情况
[1, 0, 0, 0, 1, 0, 0, 0]
此时进来一个员工入座的话,则选择最后一个座位,社交距离更大
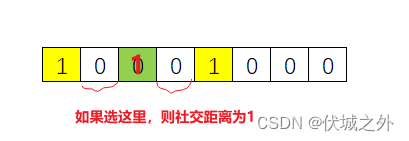
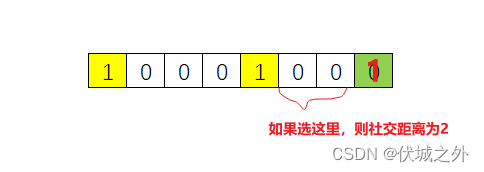
即,如果最后一个座位空闲,那么选择坐最后一个座位的社交距离计算公式是不同于之前左右边界都有人的情况的,此时最大社交距离curSeatDis为:
curSeatDis = seatNum – 1 – seatIdx.getLast – 1
我们应该考虑到这种情况。
另外,本题还需要考虑坐满的情况。更多细节请看代码实现。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const seatNum = parseInt(await readline());
const seatOrLeave = JSON.parse(await readline());
console.log(getResult(seatNum, seatOrLeave));
})();
function getResult(seatNum, seatOrLeave) {
// 记录已经坐人位置的序号
let seatIdx = [];
// 记录题解
let lastSeatIdx = -1;
// 遍历员工的进出顺序
for (let info of seatOrLeave) {
// 如果当前元素值为负数,表示出场(特殊:位置 0 的员工不会离开)
// 例如 -4 表示坐在位置 4 的员工离开(保证有员工坐在该座位上)
if (info < 0) {
const leaveIdx = -info;
seatIdx = seatIdx.filter((idx) => idx != leaveIdx);
continue;
}
// 如果当前元素值为 1,表示进场
// 如果没有空闲位置,则坐不下
if (seatIdx.length == seatNum) {
lastSeatIdx = -1;
continue;
}
if (seatIdx.length == 0) {
// 当前人员进场前,座位上没有人,则当前人员是第一个进场的,直接坐第0个位置
seatIdx.push(0);
lastSeatIdx = 0;
} else if (seatIdx.length == 1) {
// 当前人员进场前,座位上只有一个人,那么这个人肯定坐在第0个位置,则当前进场的人坐在 seatNum - 1 位置才能离 0 位置最远
seatIdx.push(seatNum - 1);
lastSeatIdx = seatNum - 1;
} else {
// 记录具有最大社交距离的座位号
let bestSeatIdx = -1;
// 记录最大社交距离
let bestSeatDis = -1;
let left = seatIdx[0]; // 左边界
for (let i = 1; i < seatIdx.length; i++) {
const right = seatIdx[i]; // 右边界
// 连续空闲座位区域的长度
const dis = right - left - 1;
// 如果连续空闲座位区域长度为0,则无法坐人,此时遍历下一个连续空闲座位区域
// 如果连续空闲座位区域长度大于0,则可以坐人
if (dis > 0) {
// 当前空闲区域能产生的最大社交距离
const curSeatDis = Math.floor(dis / 2) - (dis % 2 == 0 ? 1 : 0);
// 当前空闲区域中具备最大社交距离的位置
const curSeatIdx = left + curSeatDis + 1;
// 保留最优解
if (curSeatDis > bestSeatDis) {
bestSeatDis = curSeatDis;
bestSeatIdx = curSeatIdx;
}
}
left = right;
}
// 如果最后一个座位,即第 seatNum - 1 号座位没有坐人的话,比如 1 0 0 0 1 0 0 0 0,此时最后一段空闲区域是没有右边界的,需要特殊处理
if (seatIdx.at(-1) < seatNum - 1) {
// 此时可以直接坐到第 seatNum - 1 号座位,最大社交距离为 curSeatDis
const curSeatDis = seatNum - 1 - seatIdx.at(-1) - 1;
const curSeatIdx = seatNum - 1;
// 保留最优解
if (curSeatDis > bestSeatDis) {
bestSeatIdx = curSeatIdx;
}
}
// 如果能坐人,则将坐的位置加入seatIdx中
if (bestSeatIdx > 0) {
seatIdx.push(bestSeatIdx);
seatIdx.sort((a, b) => a - b);
}
// 假设当前人就是最后一个人,那么无论当前人是否能坐进去,都更新lastSeatIdx = bestSeatIdx
lastSeatIdx = bestSeatIdx;
}
}
return lastSeatIdx;
}
Java算法源码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int seatNum = Integer.parseInt(sc.nextLine());
String tmp = sc.nextLine();
int[] searOrLeave =
Arrays.stream(tmp.substring(1, tmp.length() - 1).split(", "))
.mapToInt(Integer::parseInt)
.toArray();
System.out.println(getResult(seatNum, searOrLeave));
}
public static int getResult(int seatNum, int[] seatOrLeave) {
// 记录已经坐人位置的序号
ArrayList<Integer> seatIdx = new ArrayList<>();
// 记录题解
int lastSeatIdx = -1;
// 遍历员工的进出顺序
for (int info : seatOrLeave) {
// 如果当前元素值为负数,表示出场(特殊:位置 0 的员工不会离开)
// 例如 -4 表示坐在位置 4 的员工离开(保证有员工坐在该座位上)
if (info < 0) {
int leaveIdx = -info;
seatIdx.remove(new Integer(leaveIdx));
continue;
}
// 如果当前元素值为 1,表示进场
// 如果没有空闲位置,则坐不下
if (seatIdx.size() == seatNum) {
// 假设当前人就是最后一个人
lastSeatIdx = -1;
continue;
}
if (seatIdx.size() == 0) {
// 当前人员进场前,座位上没有人,则当前人员是第一个进场的,直接坐第0个位置
seatIdx.add(0);
lastSeatIdx = 0;
} else if (seatIdx.size() == 1) {
// 当前人员进场前,座位上只有一个人,那么这个人肯定坐在第0个位置,则当前进场的人坐在 seatNum - 1 位置才能离 0 位置最远
seatIdx.add(seatNum - 1);
lastSeatIdx = seatNum - 1;
} else {
// 记录具有最大社交距离的座位号
int bestSeatIdx = -1;
// 记录最大社交距离
int bestSeatDis = -1;
// 找到连续空闲座位区域(该区域左、右边界是坐了人的座位)
int left = seatIdx.get(0); // 左边界
for (int i = 1; i < seatIdx.size(); i++) {
int right = seatIdx.get(i); // 右边界
// 连续空闲座位区域的长度
int dis = right - left - 1;
// 如果连续空闲座位区域长度为0,则无法坐人,此时遍历下一个连续空闲座位区域
// 如果连续空闲座位区域长度大于0,则可以坐人
if (dis > 0) {
// 当前空闲区域能产生的最大社交距离
int curSeatDis = dis / 2 - (dis % 2 == 0 ? 1 : 0);
// 当前空闲区域中具备最大社交距离的位置
int curSeatIdx = left + curSeatDis + 1;
// 保留最优解
if (curSeatDis > bestSeatDis) {
bestSeatDis = curSeatDis;
bestSeatIdx = curSeatIdx;
}
}
left = right;
}
// 如果最后一个座位,即第 seatNum - 1 号座位没有坐人的话,比如 1 0 0 0 1 0 0 0 0,此时最后一段空闲区域是没有右边界的,需要特殊处理
if (seatIdx.get(seatIdx.size() - 1) < seatNum - 1) {
// 此时可以直接坐到第 seatNum - 1 号座位,最大社交距离为 curSeatDis
int curSeatDis = seatNum - 1 - seatIdx.get(seatIdx.size() - 1) - 1;
int curSeatIdx = seatNum - 1;
// 保留最优解
if (curSeatDis > bestSeatDis) {
bestSeatIdx = curSeatIdx;
}
}
// 如果能坐人,则将坐的位置加入seatIdx中
if (bestSeatIdx > 0) {
seatIdx.add(bestSeatIdx);
seatIdx.sort((a, b) -> a - b);
}
// 假设当前人就是最后一个人,那么无论当前人是否能坐进去,都更新lastSeatIdx = bestSeatIdx
lastSeatIdx = bestSeatIdx;
}
}
return lastSeatIdx;
}
}
Python算法源码
# 输入获取
seatNum = int(input())
seatOrLeave = eval(input())
# 算法入口
def getResult():
# 记录已经坐人位置的序号
seatIdx = []
# 记录题解
lastSeatIdx = -1
# 遍历员工的进出顺序
for info in seatOrLeave:
# 如果当前元素值为负数,表示出场(特殊:位置 0 的员工不会离开)
# 例如 -4 表示坐在位置 4 的员工离开(保证有员工坐在该座位上)
if info < 0:
leaveIdx = -info
seatIdx.remove(leaveIdx)
continue
# 如果当前元素值为 1,表示进场
# 如果没有空闲位置,则坐不下
if len(seatIdx) == seatNum:
lastSeatIdx = -1
continue
if len(seatIdx) == 0:
# 当前人员进场前,座位上没有人,则当前人员是第一个进场的,直接坐第0个位置
seatIdx.append(0)
lastSeatIdx = 0
elif len(seatIdx) == 1:
# 当前人员进场前,座位上只有一个人,那么这个人肯定坐在第0个位置,则当前进场的人坐在 seatNum - 1 位置才能离 0 位置最远
seatIdx.append(seatNum - 1)
lastSeatIdx = seatNum - 1
else:
# 记录具有最大社交距离的座位号
bestSeatIdx = -1
# 记录最大社交距离
bestSeatDis = -1
# 找到连续空闲座位区域(该区域左、右边界是坐了人的座位)
left = seatIdx[0] # 左边界
for i in range(1, len(seatIdx)):
right = seatIdx[i] # 右边界
# 连续空闲座位区域的长度
dis = right - left - 1
# 如果连续空闲座位区域长度为0,则无法坐人,此时遍历下一个连续空闲座位区域
# 如果连续空闲座位区域长度大于0,则可以坐人
if dis > 0:
# 当前空闲区域能产生的最大社交距离
curSeatDis = dis // 2 - (1 if dis % 2 == 0 else 0)
# 当前空闲区域中具备最大社交距离的位置
curSeatIdx = left + curSeatDis + 1
# 保留最优解
if curSeatDis > bestSeatDis:
bestSeatDis = curSeatDis
bestSeatIdx = curSeatIdx
left = right
# 如果最后一个座位,即第 seatNum - 1 号座位没有坐人的话,比如 1 0 0 0 1 0 0 0 0,此时最后一段空闲区域是没有右边界的,需要特殊处理
if seatIdx[-1] < seatNum - 1:
# 此时可以直接坐到第 seatNum - 1 号座位,最大社交距离为 curSeatDis
curSeatDis = seatNum - 1 - seatIdx[-1] - 1
curSeatIdx = seatNum - 1
# 保留最优解
if curSeatDis > bestSeatDis:
bestSeatIdx = curSeatIdx
# 如果能坐人,则将坐的位置加入seatIdx中
if bestSeatIdx > 0:
seatIdx.append(bestSeatIdx)
seatIdx.sort()
# 假设当前人就是最后一个人,那么无论当前人是否能坐进去,都更新lastSeatIdx = bestSeatIdx
lastSeatIdx = bestSeatIdx
return lastSeatIdx
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 500
int cmp(const void *a, const void *b) {
return *((int *) a) - *((int *) b);
}
int main() {
int seatNum;
scanf("%d", &seatNum);
getchar();
int seatOrLeave[MAX_SIZE] = {0};
int seatOrLeave_size = 0;
while (scanf("[%d", &seatOrLeave[seatOrLeave_size]) || scanf("%d", &seatOrLeave[seatOrLeave_size])) {
seatOrLeave_size++;
if (getchar() != ',') break;
}
// 记录已经坐人位置的序号
int seatIdx[MAX_SIZE];
int seatIdx_size = 0;
// 记录题解
int lastSeatIdx = -1;
// 遍历员工的进出顺序
for (int i = 0; i < seatOrLeave_size; i++) {
int info = seatOrLeave[i];
// 如果当前元素值为负数,表示出场(特殊:位置 0 的员工不会离开)
// 例如 -4 表示坐在位置 4 的员工离开(保证有员工坐在该座位上)
if (info < 0) {
int leaveIdx = -info;
// 删除seatIdx中对应leaveIdx
int j = 0;
for (; j < seatIdx_size; j++) {
if (seatIdx[j] == leaveIdx) break;
}
for (; j < seatIdx_size - 1; j++) {
seatIdx[j] = seatIdx[j + 1];
}
seatIdx_size--;
continue;
}
// 如果当前元素值为 1,表示进场
// 如果没有空闲位置,则坐不下
if(seatIdx_size == seatNum) {
// 假设当前人就是最后一个人
lastSeatIdx = -1;
continue;
}
if (seatIdx_size == 0) {
// 当前人员进场前,座位上没有人,则当前人员是第一个进场的,直接坐第0个位置
seatIdx[seatIdx_size++] = 0;
lastSeatIdx = 0;
} else if (seatIdx_size == 1) {
// 当前人员进场前,座位上只有一个人,那么这个人肯定坐在第0个位置,则当前进场的人坐在 seatNum - 1 位置才能离 0 位置最远
seatIdx[seatIdx_size++] = seatNum - 1;
lastSeatIdx = seatNum - 1;
} else {
// 记录具有最大社交距离的座位号
int bestSeatIdx = -1;
// 记录最大社交距离
int bestSeatDis = -1;
// 找到连续空闲座位区域(该区域左、右边界是坐了人的座位)
int left = seatIdx[0]; // 左边界
for (int j = 1; j < seatIdx_size; j++) {
int right = seatIdx[j]; // 右边界
// 连续空闲座位区域的长度
int dis = right - left - 1;
// 如果连续空闲座位区域长度为0,则无法坐人,此时遍历下一个连续空闲座位区域
// 如果连续空闲座位区域长度大于0,则可以坐人
if (dis > 0) {
// 当前空闲区域能产生的最大社交距离
int curSeatDis = dis / 2 - (dis % 2 == 0 ? 1 : 0);
// 当前空闲区域中具备最大社交距离的位置
int curSeatIdx = left + curSeatDis + 1;
// 保留最优解
if (curSeatDis > bestSeatDis) {
bestSeatDis = curSeatDis;
bestSeatIdx = curSeatIdx;
}
}
left = right;
}
// 如果最后一个座位,即第 seatNum - 1 号座位没有坐人的话,比如 1 0 0 0 1 0 0 0 0,此时最后一段空闲区域是没有右
if (seatIdx[seatIdx_size - 1] < seatNum - 1) {
// 此时可以直接坐到第 seatNum - 1 号座位,最大社交距离为 curSeatDis
int curSeatDis = seatNum - 1 - seatIdx[seatIdx_size - 1] - 1;
int curSeatIdx = seatNum - 1;
// 保留最优解
if (curSeatDis > bestSeatDis) {
bestSeatIdx = curSeatIdx;
}
}
// 如果能坐人,则将坐的位置加入seatIdx中
if (bestSeatIdx > 0) {
seatIdx[seatIdx_size++] = bestSeatIdx;
qsort(seatIdx, seatIdx_size, sizeof(int), cmp);
}
// 假设当前人就是最后一个人,那么无论当前人是否能坐进去,都更新lastSeatIdx = bestSeatIdx
lastSeatIdx = bestSeatIdx;
}
}
printf("%dn", lastSeatIdx);
return 0;
}免责声明:
评论0