题目描述
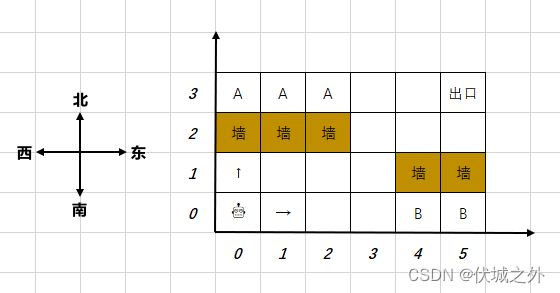
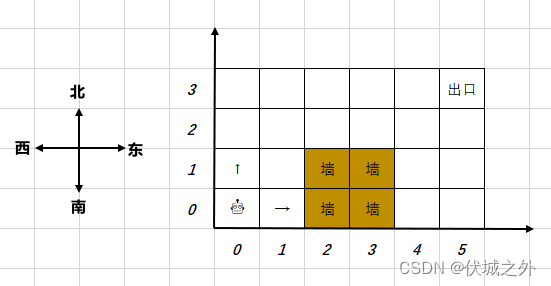
- 房间由XY的方格组成,例如下图为6*4的大小。每一个方格以坐标(x,y)描述。
- 机器人固定从方格(0,0)出发,只能向东或者向北前进。出口固定为房间的最东北角,如下图的方格(5,3)。用例保证机器人可以从入口走到出口。
- 房间有些方格是墙壁,如(4,1),机器人不能经过那儿。
- 有些地方是一旦到达就无法走到出口的,如标记为B的方格,称之为陷阱方格。
- 有些地方是机器人无法到达的的,如标记为A的方格,称之为不可达方格,不可达方格不包括墙壁所在的位置。
- 如下示例图中,陷阱方格有2个,不可达方格有3个。
- 请为该机器人实现路径规划功能:给定房间大小、墙壁位置,请计算出陷阱方格与不可达方格分别有多少个。
输入描述
- 第一行为房间的X和Y(0 < X,Y <= 1000)
- 第二行为房间中墙壁的个数N(0 <= N < X*Y)
- 接着下面会有N行墙壁的坐标
同一行中如果有多个数据以一个空格隔开,用例保证所有的输入数据均合法。(结尾不带回车换行)
输出描述
陷阱方格与不可达方格数量,两个信息在一行中输出,以一个空格隔开。(结尾不带回车换行)
用例
| 输入 |
6 4 |
| 输出 | 2 3 |
| 说明 | 该输入对应上图示例中的迷宫,陷阱方格有2个,不可达方格有3个 |
| 输入 |
6 4 |
| 输出 | 0 4 |
| 说明 |
该输入对应的迷宫如下图,没有陷阱方格,不可达方格有4个,分别是(4,0) (4,1) (5,0) (5,1)
|
题目解析
本题要求的并不是入口到出口的路径,而是找陷阱位置和不可达位置。
陷阱位置的特点是,它的北边位置和东边位置都是死路,我们可以认为越界位置和墙位置是死路,另外陷阱本身也是死路。
不可达位置的特点是,从起点位置开始,只能朝东或者朝北进行dfs,到过的点就标记一下,如果dfs结束,矩阵中任然存在着未被标记过的点,那么就是不可达点。
了解了陷阱和不可达位置特点后,我们就可以开始初始化地图了,初始化地图主要是为了标记出墙的位置和非墙位置。我们用1标记墙,用0标记非墙。
另外地图我们应该这样看:
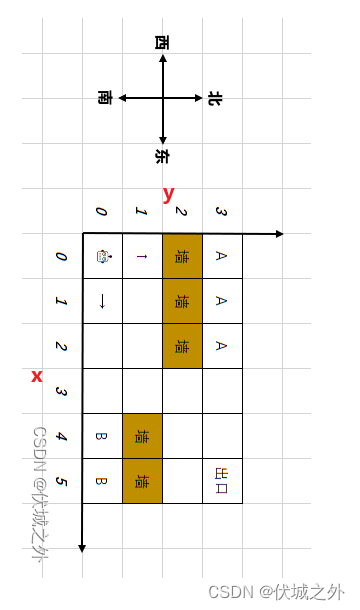
这样的话,x就是矩阵的行数,y就是矩阵的列数
比如,根据用例1初始化完地图后,如下图所示
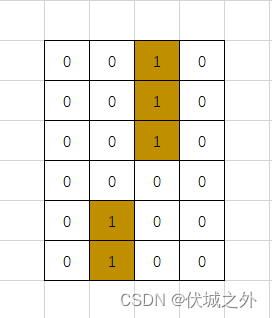
下面我们要做的工作是,从起点开始dfs,即找起点的 东边点(下边)以及北边点(右边)
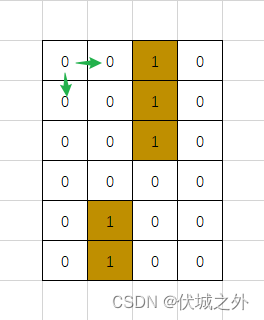
如果这东边点和北边点有一个可达,那么起点就可达。但是我们并不知道这两个点是否可达,因此将这两个进行dfs
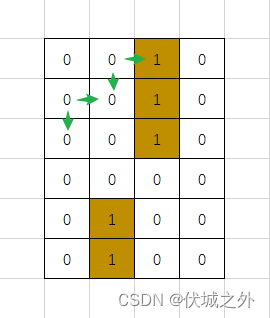
如果发现当前点的东点和北点都是死路,则当前点就是死路,如果只有一边是死路,则不能说明什么,即还需要继续dfs。当然,死路点不需要dfs。
最终,我们必然会dfs到终点位置
如果根据前面判断逻辑,则此时终点的东边、北边都是死路,因此会错误判断终点也是死路,从而影响前面所有的点,因此,我们在从起点dfs之前,就要将终点位置设为活路,即标记为2
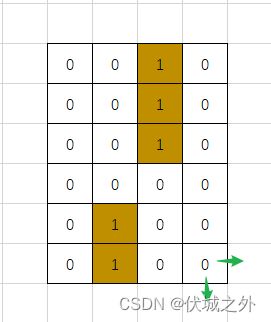
这样的话,就可以正确影响前面的点了
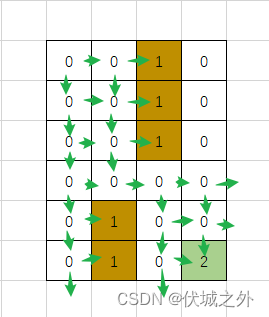
最终得到如下图
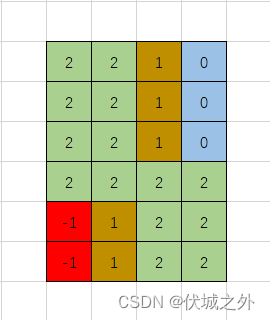
矩阵中,-1值的元素个数作为陷阱数量,0值的元素个数作为不可达数量
2023.06.16
本题Python代码可能会出现递归过深而报错的情况,注意是递归过深,而不是Stack Overflow,因此我们可以适当增大Python递归的最大深度限制,如下面代码色湖之最大递归深度为2500
import sys sys.setrecursionlimit(2500)
JavaScript算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let x, y, n, poses;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 2) {
[x, y] = lines[0].split(" ").map(Number);
n = lines[1] - 0;
}
if (n !== undefined && lines.length === n + 2) {
poses = lines.slice(2).map((line) => line.split(" ").map(Number));
console.log(getResult());
lines.length = 0;
}
});
function getResult() {
const matrix = new Array(x).fill(0).map(() => new Array(y).fill(0));
for (let [i, j] of poses) {
matrix[i][j] = 1; // 墙标记为1,非墙标记为0
}
matrix[x - 1][y - 1] = 2; // 可达点标记为2
dfs(0, 0, matrix);
let trap = 0; // 陷阱数量
let unreach = 0; // 不可达点数量
for (let i = 0; i < x; i++) {
for (let j = 0; j < y; j++) {
if (matrix[i][j] == 0) unreach++;
else if (matrix[i][j] == -1) trap++;
}
}
return `${trap} ${unreach}`;
}
function dfs(cx, cy, matrix) {
if (cx >= x || cy >= y) return false; // 如果下一步越界,则下一步不可达
if (matrix[cx][cy] == 1) return false; // 如果下一步为墙,则下一步不可达
if (matrix[cx][cy] == -1) return false; // 如果下一步为不可达点,则下一步不可达
if (matrix[cx][cy] == 2) return true; // 如果下一步为可达点,则下一步可达
if (matrix[cx][cy] == 0) {
const east = dfs(cx + 1, cy, matrix); // 向东走下一步
const north = dfs(cx, cy + 1, matrix); // 向北走下一步
if (east || north) {
matrix[cx][cy] = 2; // 如果向东可达或者向北可达,则当前点可达,标记2
} else {
matrix[cx][cy] = -1; // 如果向东,向北都不可达,则当前前也是不可达点,标记-1
}
}
return matrix[cx][cy] == 2;
}
Java算法源码
import java.util.Scanner;
public class Main {
static int x;
static int y;
static int n;
static int[][] poses;
static int[][] matrix;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
x = sc.nextInt(); // 行数
y = sc.nextInt(); // 列数
n = sc.nextInt(); // 墙数
poses = new int[n][2]; // 墙位置
for (int i = 0; i < n; i++) {
poses[i][0] = sc.nextInt();
poses[i][1] = sc.nextInt();
}
getResult();
}
public static void getResult() {
matrix = new int[x][y];
for (int[] pos : poses) {
int i = pos[0];
int j = pos[1];
matrix[i][j] = 1; // 墙点值为1,非墙点值为0
}
matrix[x - 1][y - 1] = 2; // 可达点值为2
dfs(0, 0);
int trap = 0; // 陷阱数量
int unreach = 0; // 不可达点数量
for (int i = 0; i < x; i++) {
for (int j = 0; j < y; j++) {
if (matrix[i][j] == 0) unreach++;
else if (matrix[i][j] == -1) trap++;
}
}
System.out.println(trap + " " + unreach);
}
public static boolean dfs(int cx, int cy) {
if (cx >= x || cy >= y) return false;
if (matrix[cx][cy] == 1) return false;
if (matrix[cx][cy] == -1) return false;
if (matrix[cx][cy] == 2) return true;
if (matrix[cx][cy] == 0) {
boolean east = dfs(cx + 1, cy);
boolean north = dfs(cx, cy + 1);
if (east || north) {
matrix[cx][cy] = 2; // 如果向东可达或者向北可达,则当前点可达,将值设为2
} else {
matrix[cx][cy] = -1; // 如果向东,向北都不可达,则当前前也是不可达点,将值设为-1
}
}
return matrix[cx][cy] == 2;
}
}
Python算法源码
import sys
sys.setrecursionlimit(2500)
# 输入获取
x, y = map(int, input().split())
n = int(input())
poses = [list(map(int, input().split())) for _ in range(n)]
# 深搜
def dfs(cx, cy, matrix):
if cx >= x or cy >= y:
return False
if matrix[cx][cy] == 1: # 如果下一步为墙,则下一步不可达
return False
if matrix[cx][cy] == -1: # 如果下一步为不可达点,则下一步不可达
return False
if matrix[cx][cy] == 2: # 如果下一步为可达点,则下一步可达
return True
if matrix[cx][cy] == 0:
east = dfs(cx + 1, cy, matrix) # 向东走下一步
north = dfs(cx, cy + 1, matrix) # 下北走下一步
if east or north:
matrix[cx][cy] = 2 # 如果向东可达或者向北可达,则当前点可达,标记2
else:
matrix[cx][cy] = -1 # 如果向东,向北都不可达,则当前前也是不可达点,标记-1
return matrix[cx][cy] == 2
# 算法入口
def getResult():
matrix = [[0 for _ in range(y)] for _ in range(x)]
for i, j in poses:
matrix[i][j] = 1 # 墙标记为1,非墙标记为0
matrix[x - 1][y - 1] = 2 # 可达点标记为2
dfs(0, 0, matrix)
trap = 0 # 陷阱数量
unreach = 0 # 不可达点数量
for i in range(x):
for j in range(y):
if matrix[i][j] == 0:
unreach += 1
elif matrix[i][j] == -1:
trap += 1
return f"{trap} {unreach}"
# 算法调用
print(getResult())
免责声明:
评论0