题目描述
一个局域网内有很多台电脑,分别标注为 0 ~ N-1 的数字。相连接的电脑距离不一样,所以感染时间不一样,感染时间用 t 表示。
其中网络内一台电脑被病毒感染,求其感染网络内所有的电脑最少需要多长时间。如果最后有电脑不会感染,则返回-1。
给定一个数组 times 表示一台电脑把相邻电脑感染所用的时间。
如图:path[i] = {i, j, t} 表示:电脑 i->j,电脑 i 上的病毒感染 j,需要时间 t。
输入描述
4
3
2 1 1
2 3 1
3 4 1
2
输出描述
2
用例
| 输入 | 4 3 2 1 1 2 3 1 3 4 1 2 |
| 输出 | 2 |
| 说明 |
第一个参数:局域网内电脑个数N,1 ≤ N ≤ 200; 第二个参数:总共多少条网络连接 第三个 2 1 1 表示2->1时间为1 第六行:表示病毒最开始所在电脑号2 |
题目解析
用例图示如下
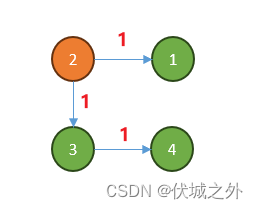
病毒源头是2,其中:
2->1需要时间1
2->3需要时间1,3->4需要时间1
因此最少需要时间2才能感染所有电脑。
本题考察的是单源最短路径求解,解析可以参考:
另外,本题题目描述和用例不符。因为题目说:
一个局域网内有很多台电脑,分别标注为 0 ~ N-1 的数字。
但是题目用例,第一行给出N=4,但是第五行出现了电脑编号也是4的情况。
这影响到了下面代码中dist、visited数组长度的定义。当前代码实现以用例数据为准,即认为电脑编号是 1~N。
具体考试时需要随机应变。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const n = parseInt(await readline());
// 邻接表
const graph = {};
const m = parseInt(await readline());
for (let i = 0; i < m; i++) {
// [出发点, 目标点, 出发点到达目标点的耗时]
const [u, v, w] = (await readline()).split(" ").map(Number);
if (graph[u]) {
graph[u].push([v, w]);
} else {
graph[u] = [[v, w]];
}
}
// 记录源点到其他各点的最短耗时
// 初始时,假设源点不可达其他剩余点,即源点到达其他点的耗时无限大
const dist = new Array(n + 1).fill(Infinity);
// 源点
const src = parseInt(await readline());
// 源点到达源点的耗时为0
dist[src] = 0;
// needCheck中记录的其实是:已被探索过的路径的终点(路径指的是源点->终点)
// 排序规则是,路径终点的权重(即源点->终点的耗时)越小越靠后
const needCheck = [];
// 初始被探索过的路径只有源点本身
needCheck.push(src);
// 记录对应点是否在needCheck中
const visited = new Array(n + 1).fill(false);
visited[src] = true;
while (needCheck.length > 0) {
// 取出最优路径的终点(耗时最少的路径)作为新的起点
const cur = needCheck.pop();
visited[cur] = false;
// 如果cur有可达的其他点
if (graph[cur]) {
// v是可达的其他店
// w是cur->v的耗时
for (let [v, w] of graph[cur]) {
// 那么如果从源点到cur点的耗时是dist[cur],那么源点到v点的耗时就是dist[cur] + w
const newDist = dist[cur] + w;
// 而源点到v的耗时之前是dist[v],因此如果newDist < dist[v],则找到更少耗时的路径
if (dist[v] > newDist) {
// 更新源点到v的路径,即更新v点权重
dist[v] = newDist;
// 如果v点不在needCheck中,则加入,因为v作为终点的路径需要加入到下一次最优路径的评比中
if (!visited[v]) {
visited[v] = true;
needCheck.push(v);
needCheck.sort((a, b) => dist[b] - dist[a]);
}
}
}
}
}
// dist记录的是源点到达其他各点的最短耗时,我们取出其中最大的就是源点走完所有点的最短耗时
let ans = 0;
for (let i = 1; i <= n; i++) {
ans = Math.max(ans, dist[i]);
}
// 如果存在某个点无法到达,则源点到该点的耗时为Integer.MAX_VALUE
console.log(ans == Infinity ? -1 : ans);
})();
Java算法源码
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
// 邻接表
HashMap<Integer, ArrayList<int[]>> graph = new HashMap<>();
int m = sc.nextInt();
for (int i = 0; i < m; i++) {
int u = sc.nextInt(); // 出发点
int v = sc.nextInt(); // 目标点
int w = sc.nextInt(); // 出发点到达目标点的耗时
graph.putIfAbsent(u, new ArrayList<>());
graph.get(u).add(new int[] {v, w});
}
// 记录源点到其他剩余的最短耗时
int[] dist = new int[n + 1];
// 初始时,假设源点不可达其他剩余点,即源点到达其他点的耗时无限大
Arrays.fill(dist, Integer.MAX_VALUE);
// 源点
int src = sc.nextInt();
// 源点到达源点的耗时为0
dist[src] = 0;
// 优先队列needCheck中记录的其实是:已被探索过的路径的终点(路径指的是源点->终点)
// 优先队列优先级规则是,路径终点的权重(即源点->终点的耗时)越小越优先
PriorityQueue<Integer> needCheck = new PriorityQueue<>((a, b) -> dist[a] - dist[b]);
// 初始被探索过的路径只有源点本身
needCheck.add(src);
// 记录对应点是否在needCheck中
boolean[] visited = new boolean[n + 1];
visited[src] = true;
while (needCheck.size() > 0) {
// 取出最优路径的终点(耗时最少的路径)作为新的起点
int cur = needCheck.poll();
visited[cur] = false;
// 如果cur有可达的其他点
if (graph.containsKey(cur)) {
for (int[] next : graph.get(cur)) {
// v是可达的其他店
// w是cur->v的耗时
int v = next[0], w = next[1];
// 那么如果从源点到cur点的耗时是dist[cur],那么源点到v点的耗时就是dist[cur] + w
int newDist = dist[cur] + w;
// 而源点到v的耗时之前是dist[v],因此如果newDist < dist[v],则找到更少耗时的路径
if (dist[v] > newDist) {
// 更新源点到v的路径,即更新v点权重
dist[v] = newDist;
// 如果v点不在needCheck中,则加入,因为v作为终点的路径需要加入到下一次最优路径的评比中
if (!visited[v]) {
visited[v] = true;
needCheck.add(v);
}
}
}
}
}
// dist记录的是源点到达其他各点的最短耗时,我们取出其中最大的就是源点走完所有点的最短耗时
int ans = 0;
for (int i = 1; i <= n; i++) {
ans = Math.max(ans, dist[i]);
}
// 如果存在某个点无法到达,则源点到该点的耗时为Integer.MAX_VALUE
System.out.println(ans == Integer.MAX_VALUE ? -1 : ans);
}
}
Python算法源码
import sys
# 输入获取
n = int(input())
# 邻接表
graph = {}
m = int(input())
for i in range(m):
# 出发点, 目标点, 出发点到达目标点的耗时
u, v, w = map(int, input().split())
graph.setdefault(u, [])
graph[u].append([v, w])
# 记录源点到其他各点的最短耗时
# 初始时,假设源点不可达其他剩余点,即源点到达其他点的耗时无限大
dist = [sys.maxsize] * (n+1)
# 源点
src = int(input())
# 源点到达源点的耗时为0
dist[src] = 0
# needCheck中记录的其实是:已被探索过的路径的终点(路径指的是源点->终点)
# 排序规则是,路径终点的权重(即源点->终点的耗时)越小越靠后
# 初始被探索过的路径只有源点本身
needCheck = [src]
# 记录对应点是否在needCheck中
visited = [False] * (n+1)
visited[src] = True
while len(needCheck) > 0:
# 取出最优路径的终点(耗时最少的路径)作为新的起点
cur = needCheck.pop()
visited[cur] = False
# 如果cur有可达的其他点
if graph.get(cur) is not None:
# v是可达的其他店,w是cur->v的耗时
for v, w in graph[cur]:
# 那么如果从源点到cur点的耗时是dist[cur],那么源点到v点的耗时就是dist[cur] + w
newDist = dist[cur] + w
# 而源点到v的耗时之前是dist[v],因此如果newDist < dist[v],则找到更少耗时的路径
if dist[v] > newDist:
# 更新源点到v的路径,即更新v点权重
dist[v] = newDist
# 如果v点不在needCheck中,则加入,因为v作为终点的路径需要加入到下一次最优路径的评比中
if not visited[v]:
visited[v] = True
needCheck.append(v)
needCheck.sort(key=lambda x: -dist[x])
ans = max(dist[1:])
print(-1 if ans == sys.maxsize else ans)
C算法源码
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define MAX_SIZE 200
#define MAX(a,b) ((a) > (b) ? (a) : (b))
/** 链表节点 **/
typedef struct ListNode {
int v; // 目标点
int w; // 出发点到达目标点的耗时
struct ListNode *next;
} ListNode;
/** 链表 **/
typedef struct LinkedList {
int size;
ListNode *head;
ListNode *tail;
} LinkedList;
/** 初始化链表 **/
LinkedList *new_LinkedList() {
LinkedList *link = (LinkedList *) malloc(sizeof(LinkedList));
link->head = NULL;
link->tail = NULL;
link->size = 0;
return link;
}
/** 链表尾插 **/
void add_LinkedList(LinkedList *link, int v, int w) {
ListNode *node = (ListNode *) malloc(sizeof(ListNode));
node->v = v;
node->w = w;
node->next = NULL;
if (link->size == 0) {
link->head = node;
link->tail = node;
} else {
link->tail->next = node;
link->tail = node;
}
link->size++;
}
// 记录源点到其他各点的最短耗时
int dist[MAX_SIZE];
int cmp(const void* a, const void* b) {
int A = *((int*) a);
int B = *((int*) b);
return dist[B] - dist[A];
}
int main() {
int n;
scanf("%d", &n);
LinkedList **graph = (LinkedList **) calloc(n + 1, sizeof(LinkedList *));
int m;
scanf("%d", &m);
for (int i = 0; i < m; i++) {
// 出发点, 目标点, 出发点到达目标点的耗时
int u, v, w;
scanf("%d %d %d", &u, &v, &w);
if (graph[u] == NULL) {
graph[u] = new_LinkedList();
}
add_LinkedList(graph[u], v, w);
}
// 初始时,假设源点不可达其他剩余点,即源点到达其他点的耗时无限大
for (int i = 1; i <= n; i++) {
dist[i] = INT_MAX;
}
// 源点
int src;
scanf("%d", &src);
// 源点到达源点的耗时为0
dist[src] = 0;
// needCheck中记录的其实是:已被探索过的路径的终点(路径指的是源点->终点)
// 排序规则是,路径终点的权重(即源点->终点的耗时)越小越靠后
int needCheck[MAX_SIZE];
int needCheck_size = 0;
// 初始被探索过的路径只有源点本身
needCheck[0] = src;
needCheck_size++;
// 记录对应点是否在needCheck中
int visited[n + 1];
for (int i = 1; i <= n; i++) {
visited[i] = 0;
}
visited[src] = 1;
while (needCheck_size > 0) {
// 取出最优路径的终点(耗时最少的路径)作为新的起点
int cur = needCheck[needCheck_size - 1];
needCheck_size--;
visited[cur] = 0;
// 如果cur有可达的其他点
if(graph[cur] != NULL) {
ListNode* node = graph[cur]->head;
while(node != NULL) {
int v = node->v; // v是可达的其他店
int w = node->w; // w是cur->v的耗时
// 那么如果从源点到cur点的耗时是dist[cur],那么源点到v点的耗时就是dist[cur] + w
int newDist = dist[cur] + w;
// 而源点到v的耗时之前是dist[v],因此如果newDist < dist[v],则找到更少耗时的路径
if(dist[v] > newDist) {
// 更新源点到v的路径,即更新v点权重
dist[v] = newDist;
// 如果v点不在needCheck中,则加入,因为v作为终点的路径需要加入到下一次最优路径的评比中
if(!visited[v]) {
visited[v] = 1;
needCheck[needCheck_size] = v;
needCheck_size++;
qsort(needCheck, needCheck_size, sizeof(int), cmp);
}
}
node = node->next;
}
}
}
int ans = 0;
for(int i=1; i<=n; i++) {
ans = MAX(ans, dist[i]);
}
printf("%dn", ans == INT_MAX ? -1 : ans);
return 0;
}免责声明:
1、IT资源小站为非营利性网站,全站所有资料仅供网友个人学习使用,禁止商用
2、本站所有文档、视频、书籍等资料均由网友分享,本站只负责收集不承担任何技术及版权问题
3、如本帖侵犯到任何版权问题,请立即告知本站,本站将及时予与删除下载链接并致以最深的歉意
4、本帖部分内容转载自其它媒体,但并不代表本站赞同其观点和对其真实性负责
5、一经注册为本站会员,一律视为同意网站规定,本站管理员及版主有权禁止违规用户
6、其他单位或个人使用、转载或引用本文时必须同时征得该帖子作者和IT资源小站的同意
7、IT资源小站管理员和版主有权不事先通知发贴者而删除本文
评论0