题目描述
从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。
输入描述
输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150
输入格式:
N M K
N*M矩阵
输出描述
N*M 的矩阵中可以选出 M! / N! 种组合数组,每个组合数组种第 K 大的数中的最小值。无需考虑重复数字,直接取字典排序结果即可。
备注
注意:结果是第 K 大的数字的最小值
用例
| 输入 | 3 4 2 1 5 6 6 8 3 4 3 6 8 6 3 |
| 输出 | 3 |
| 说明 |
N*M的矩阵中可以选出 M!/ N!种组合数组,每个组合数组种第 K 大的数中的最小值; 上述输入中选出数组组合为: 1,3,6; 1,3,3; 1,4,8; 1,4,3; …… 上述输入样例中选出的组合数组有24种,最小数组为1,3,3,则第2大的最小值为3 |
题目解析
本题需要我们从矩阵中选取N个元素,这个N元素的特点是:任意两个不能同行同列。
而满足上面条件的N个元素存在多组,我们需要找到着各个组中第K大元素的最小值。
难点一:如何从矩阵中找到N个互相不同行同列的元素呢?
暴力枚举的话,肯定会超时,因此需要寻找更优解法。
根据要求,每行每列只能有一个元素被选择,即可以认为每个行号只能和一个列号进行配对,且配对过的列号不能再和其他行号配对,而形成了配对关系的行号,列号,其实就是一个元素的坐标位置。
因此,找N个互相不同行同列的元素,其实就是在二分图(所有行号一部分,所有列号一部分)找N个边的匹配。
如下图所示
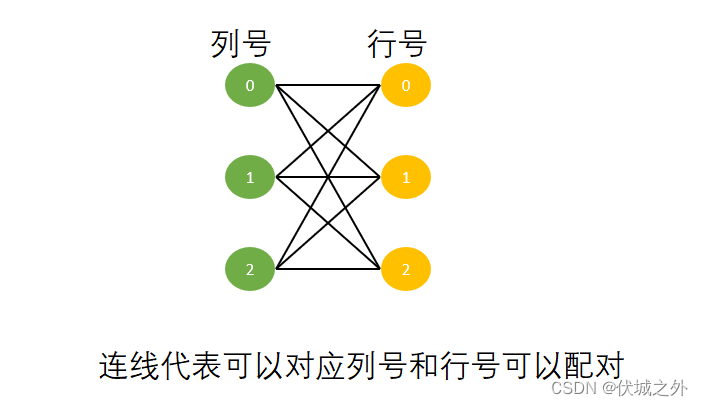
关于二分图的知识可以看下:
看完上面博客后,我们就可以继续后面说明了。
现在我们已经有了二分图了,也就可以找到具有N个边的"匹配",但是这种"匹配"可能非常多,难道要全部找出来,然后对比每个"匹配"中第K大,那不还是暴力吗?
题目需要我们多组N个元素中的第K大元素的最小取值,
换位思考一下,假设我们已经知道了第K大的最小取值是kth,那么:
- 检查矩阵中是否至多找到(N – K + 1 个) ≤ kth 的元素值,且这些元素值互不同行同列
N个数中,有K-1个数比kth大,那么相对应的有 (N – (K-1)) = (N – K + 1 ) 个数 ≤ kth。
即找的 N – K + 1 个数中包含了 kth(第K大值)本身。
而kth的大小和二分图最大匹配是正相关的,因为:
每个匹配边 其实就是 行号到列号的配对连线
而行号和列号的组合其实就是坐标位置,根据坐标位置可以得到一个矩阵元素值
因此kth越小,意味着可以找到的 ≤ kth 的矩阵元素越少,相反的,kth 越大,则找到的 ≤ kth 的矩阵元素越多。
因此kth值大小和二分图最大匹配数是线性关系,我们可以使用二分法,来枚举kth。
二分枚举的范围是:1 ~ 矩阵元素最大值,这里不用担心二分枚举到kth不是矩阵元素,因为这种情况会被过滤掉,原因是:我们要找 N – K + 1 个 <= kth 的矩阵元素,最后把关的必然是 kth 本身,即我们必然要在矩阵中找到一个 kth 值,如果二分枚举到的 kth 不是矩阵元素,则无法满足这个要求。
二分枚举到一个kth值:
- 如果kth使得二分图最大匹配 >= N-K+1 个,则说明当前kth取大了,我们应该尝试更小的kth值,即缩小二分右边界为kth-1
- 如果kth使得二分图最大匹配 < N-K+1 个,则说明当前kth取小了,我们应该继续尝试更大的kth值,即扩大二分左边界为kth+1
当二分左右边界重合时的kth值即为题解。
关于二分法,可以看下:
算法设计 – 二分法和三分法,洛谷P3382_二分法与三分法-CSDN博客
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const [n, m, k] = (await readline()).split(" ").map(Number);
let min = 1;
let max = -Infinity;
const matrix = [];
for (let i = 0; i < n; i++) {
matrix.push((await readline()).split(" ").map(Number));
max = Math.max(max, ...matrix[i]);
}
// 二分枚举第K大的最小取值
while (min <= max) {
// mid就是被枚举出来的N个数中的第K大的最小取值
const mid = (min + max) >> 1;
// 检查mid作为N个数中第K大值时,是否存在N-K+1个<=它的值
if (check(mid)) {
max = mid - 1;
} else {
min = mid + 1;
}
}
console.log(min);
function check(kth) {
// 利用二分图最大匹配来求解,小于等于kth(第K大值)的元素个数(即二分图最大匹配)
let smallerCount = 0;
// 记录每个行号的匹配成功的列号
// 初始时每个行号都处于未配对状态,此时将行号配对的列号赋值为-1
const match = new Array(m).fill(-1);
// 遍历列号,每个列号对互相心仪的行号发起配对请求
for (let i = 0; i < n; i++) {
// 记录增广路访问过的行号
const vis = new Array(m).fill(false);
if (dfs(i, kth, match, vis)) {
smallerCount++;
}
}
return smallerCount >= n - k + 1;
}
function dfs(i, kth, match, vis) {
// 列号 i 发起了配对请求
// 遍历每一个行号j
for (let j = 0; j < m; j++) {
// 如果当前行号j未被增广路探索过 && 当前行j列号i可以配对(如果行列号位置(i,j)对应矩阵元素值小于等于kth(第K大值),则可以配对)
if (!vis[j] && matrix[i][j] <= kth) {
vis[j] = true;
// 如果对应行号j未配对,或者,已配对但是配对的雷浩match[j]可以找到其他行号重新配对
if (match[j] == -1 || dfs(match[j], kth, match, vis)) {
// 则当前列号i 和 行号j 可以配对
match[j] = i;
return true;
}
}
}
return false;
}
})();
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int n;
static int m;
static int k;
static int[][] matrix;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
k = sc.nextInt();
int min = 1;
int max = Integer.MIN_VALUE;
matrix = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
matrix[i][j] = sc.nextInt();
max = Math.max(max, matrix[i][j]);
}
}
// 二分枚举第K大值
while (min <= max) {
// mid就是被枚举出来的N个数中的第K大值
int mid = (min + max) >> 1;
// 检查mid作为N个数中第K大值时,是否存在N-K+1个不大于它的值
if (check(mid)) {
max = mid - 1;
} else {
min = mid + 1;
}
}
System.out.println(min);
}
public static boolean check(int kth) {
// 利用二分图最大匹配来求解,小于等于kth(第K大值)的元素个数(即二分图最大匹配)
int smallerCount = 0;
// 记录每个行号的匹配成功的列号
int[] match = new int[m];
// 初始时每个行号都处于未配对状态,此时将行号配对的列号赋值为-1
Arrays.fill(match, -1);
// 遍历列号,每个列号对互相心仪的行号发起配对请求
for (int i = 0; i < n; i++) {
// 记录增广路访问过的行号
boolean[] vis = new boolean[m];
if (dfs(i, kth, match, vis)) smallerCount++;
}
return smallerCount >= n - k + 1;
}
public static boolean dfs(int i, int kth, int[] match, boolean[] vis) {
// 列号 i 发起了配对请求
// 遍历每一个行号j
for (int j = 0; j < m; j++) {
// 如果当前行号j未被增广路探索过 && 当前行j列号i可以配对(如果行列号位置(i,j)对应矩阵元素值小于等于kth(第K大值),则可以配对)
if (!vis[j] && matrix[i][j] <= kth) {
vis[j] = true;
// 如果对应行号j未配对,或者,已配对但是配对的雷浩match[j]可以找到其他行号重新配对
if (match[j] == -1 || dfs(match[j], kth, match, vis)) {
// 则当前列号i 和 行号j 可以配对
match[j] = i;
return true;
}
}
}
return false;
}
}
Python算法源码
import sys
# 输入获取
n, m, k = map(int, input().split())
matrix = [list(map(int, input().split())) for _ in range(n)]
def dfs(i, kth, match, vis):
# 列号 i 发起了配对请求
# 遍历每一个行号j
for j in range(m):
# 如果当前行号j未被增广路探索过 && 当前行j列号i可以配对(如果行列号位置(i,j)对应矩阵元素值小于等于kth(第K大值),则可以配对)
if not vis[j] and matrix[i][j] <= kth:
vis[j] = True
# 如果对应行号j未配对,或者,已配对但是配对的雷浩match[j]可以找到其他行号重新配对
if match[j] == -1 or dfs(match[j], kth, match, vis):
# 则当前列号i 和 行号j 可以配对
match[j] = i
return True
return False
def check(kth):
# 利用二分图最大匹配来求解,小于等于kth(第K大值)的元素个数(即二分图最大匹配)
smallerCount = 0
# 记录每个行号的匹配成功的列号
# 初始时每个行号都处于未配对状态,此时将行号配对的列号赋值为-1
match = [-1] * m
# 遍历列号,每个列号对互相心仪的行号发起配对请求
for i in range(n):
# 记录增广路访问过的行号
vis = [False] * m
if dfs(i, kth, match, vis):
smallerCount += 1
return smallerCount >= n - k + 1
# 算法入口
def getResult():
low = 1
high = -sys.maxsize
for i in range(n):
for j in range(m):
high = max(high, matrix[i][j])
# 二分枚举第K大值
while low <= high:
# mid就是被枚举出来的N个数中的第K大值
mid = (low + high) >> 1
# 检查mid作为N个数中第K大值时,是否存在N-K+1个<=它的值
if check(mid):
high = mid - 1
else:
low = mid + 1
return low
# 算法调用
print(getResult())C算法源码
#include <stdio.h>
#include <limits.h>
#include <math.h>
#define MAX_SIZE 150
#define bool int
#define TRUE 1
#define FALSE 0
int n, m, k;
int matrix[MAX_SIZE][MAX_SIZE];
bool dfs(int i, int kth, int match[], int vis[]) {
// 列号 i 发起了配对请求
// 遍历每一个行号j
for (int j = 0; j < m; j++) {
// 如果当前行号j未被增广路探索过 && 当前行j列号i可以配对(如果行列号位置(i,j)对应矩阵元素值小于等于kth(第K大值),则可以配对)
if (!vis[j] && matrix[i][j] <= kth) {
vis[j] = TRUE;
// 如果对应行号j未配对,或者,已配对但是配对的雷浩match[j]可以找到其他行号重新配对
if (match[j] == -1 || dfs(match[j], kth, match, vis)) {
// 则当前列号i 和 行号j 可以配对
match[j] = i;
return TRUE;
}
}
}
return FALSE;
}
bool check(int kth) {
// 利用二分图最大匹配来求解,小于等于kth(第K大值)的元素个数(即二分图最大匹配)
int smallerCount = 0;
// 记录每个行号的匹配成功的列号
int match[m];
// 初始时每个行号都处于未配对状态,此时将行号配对的列号赋值为-1
for (int i = 0; i < m; i++) match[i] = -1;
// 遍历列号,每个列号对互相心仪的行号发起配对请求
for (int i = 0; i < n; i++) {
// 记录增广路访问过的行号
int vis[MAX_SIZE] = {FALSE};
if (dfs(i, kth, match, vis)) {
smallerCount++;
}
}
return smallerCount >= (n - k + 1);
}
int main() {
scanf("%d %d %d", &n, &m, &k);
int min = 1;
int max = INT_MIN;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
scanf("%d", &matrix[i][j]);
max = (int) fmax(max, matrix[i][j]);
}
}
// 二分枚举第K大值
while (min <= max) {
// mid就是被枚举出来的N个数中的第K大值
int mid = (min + max) >> 1;
// 检查mid作为N个数中第K大值时,是否存在N-K+1个<=它的值
if (check(mid)) {
max = mid - 1;
} else {
min = mid + 1;
}
}
printf("%dn", min);
return 0;
}免责声明:
评论0