题目描述
给定一个表达式,求其分数计算结果。
表达式的限制如下:
- 所有的输入数字皆为正整数(包括0)
- 仅支持四则运算(+-*/)和括号
- 结果为整数或分数,分数必须化为最简格式(比如6,3/4,7/8,90/7)
- 除数可能为0,如果遇到这种情况,直接输出"ERROR"
- 输入和最终计算结果中的数字都不会超出整型范围
用例输入一定合法,不会出现括号匹配的情况
输入描述
字符串格式的表达式,仅支持+-*/,数字可能超过两位,可能带有空格,没有负数
长度小于200个字符
输出描述
表达式结果,以最简格式表达
- 如果结果为整数,那么直接输出整数
- 如果结果为负数,那么分子分母不可再约分,可以为假分数,不可表达为带分数
- 结果可能是负数,符号放在前面
用例
| 输入 | 1 + 5 * 7 / 8 |
| 输出 | 43/8 |
| 说明 | 无 |
| 输入 | 1 / (0 – 5) |
| 输出 | -1/5 |
| 说明 | 符号需要提到最前面 |
| 输入 | 1 * (3*4/(8-(7+0))) |
| 输出 | 12 |
| 说明 | 注意括号可以多重嵌套 |
题目解析
本题是经典的中缀表达式计算问题。
双栈实现中缀表达式计算
关于中缀表达式计算,通常是定义两个栈结构:
- 一个栈用于记录操作数:假设为oper_num_stack
- 一个栈用于记录操作符:假设为oper_sign_stack
下面我们通过几个例子来说明两个栈的工作原理:
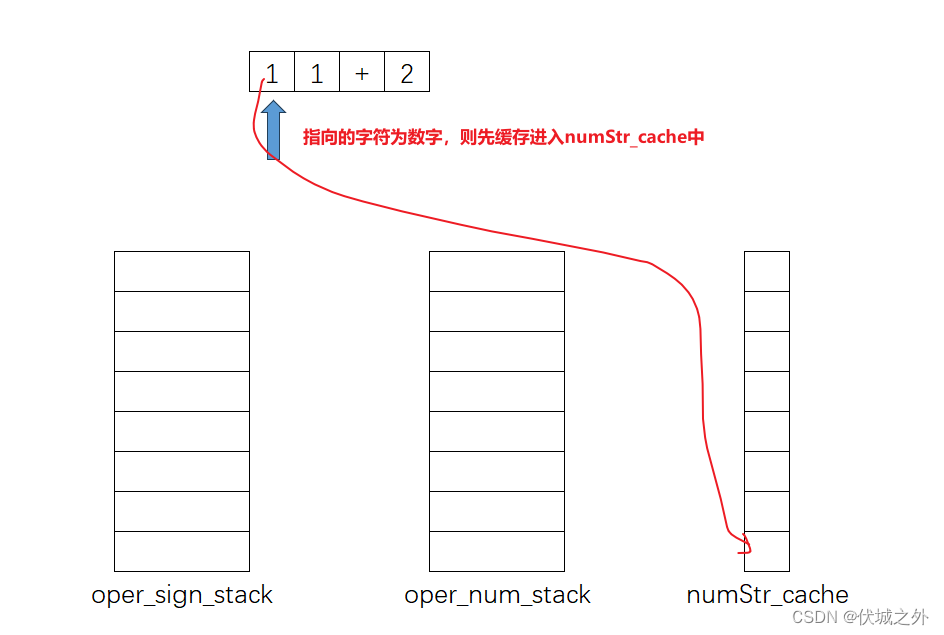
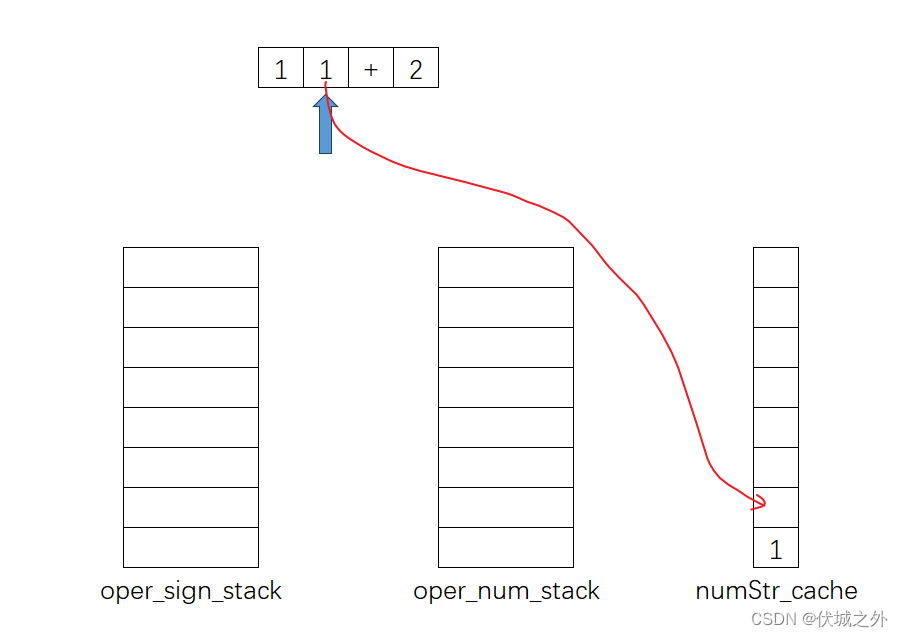
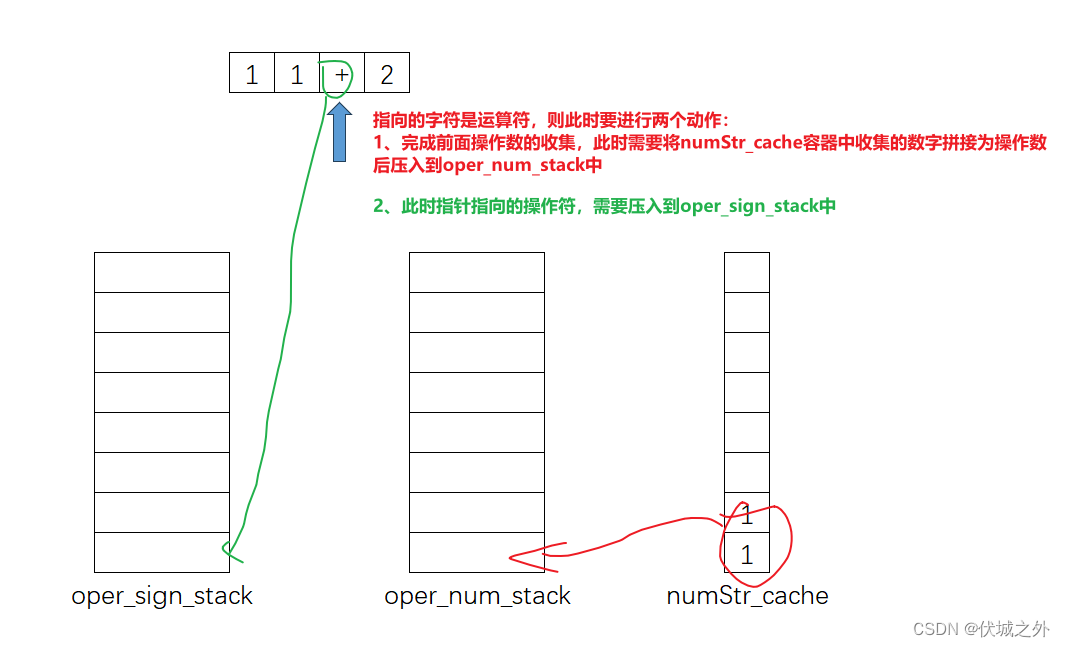
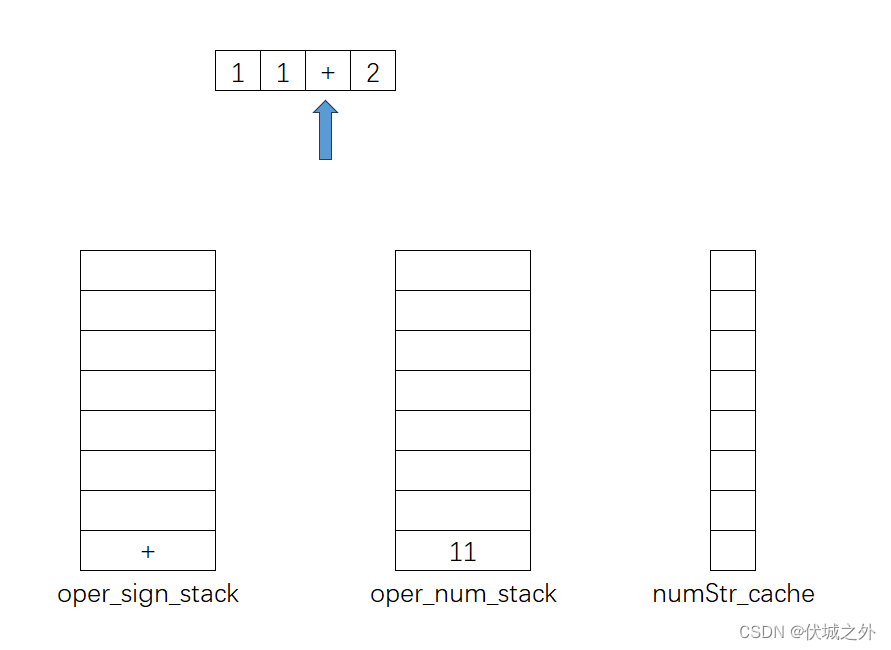
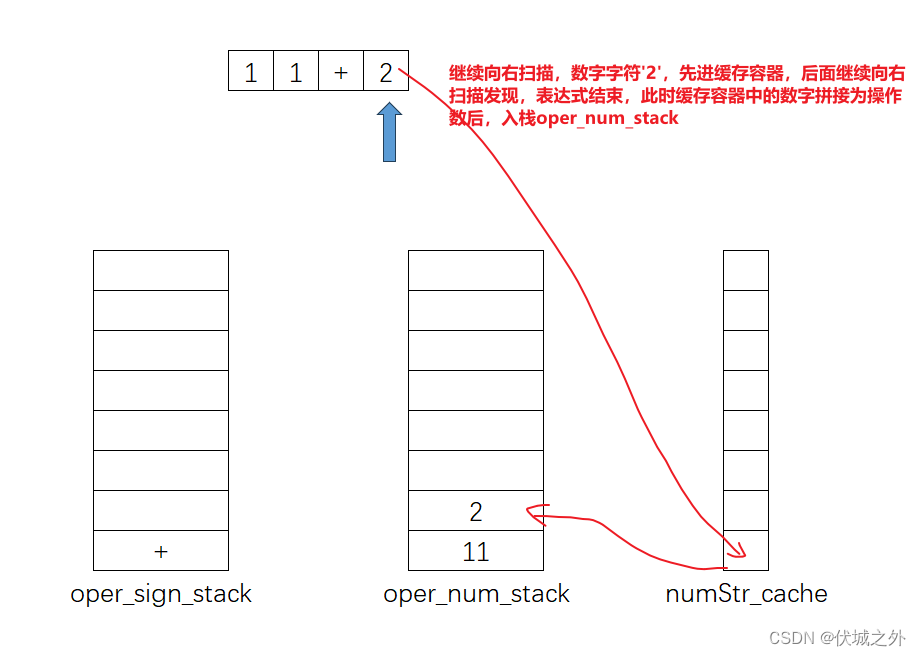
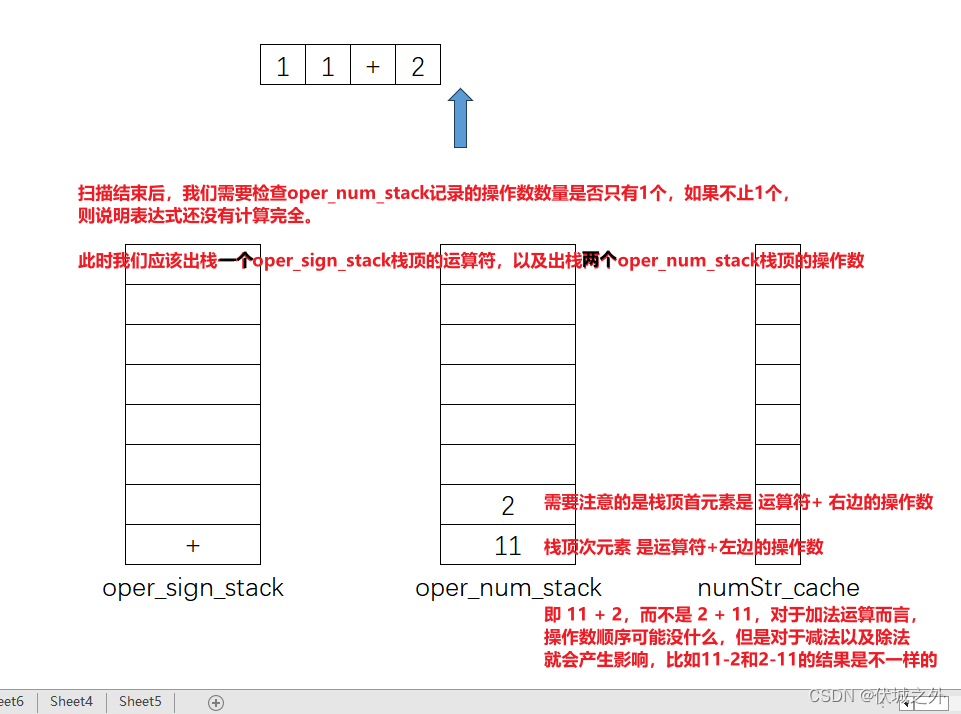
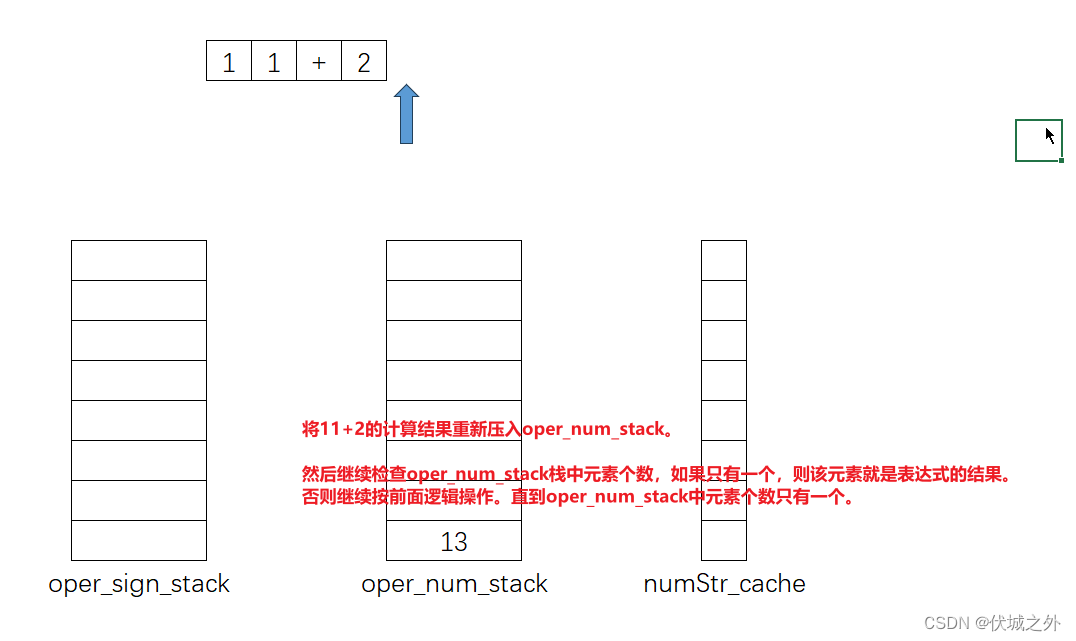
通过上面流程,我们可以发现,每次出栈oper_sign_stack一个运算符,那么就要出栈oper_num_stack两个操作数。
那么如果存在下面这种情况,是否支持这样的出栈运算逻辑呢?
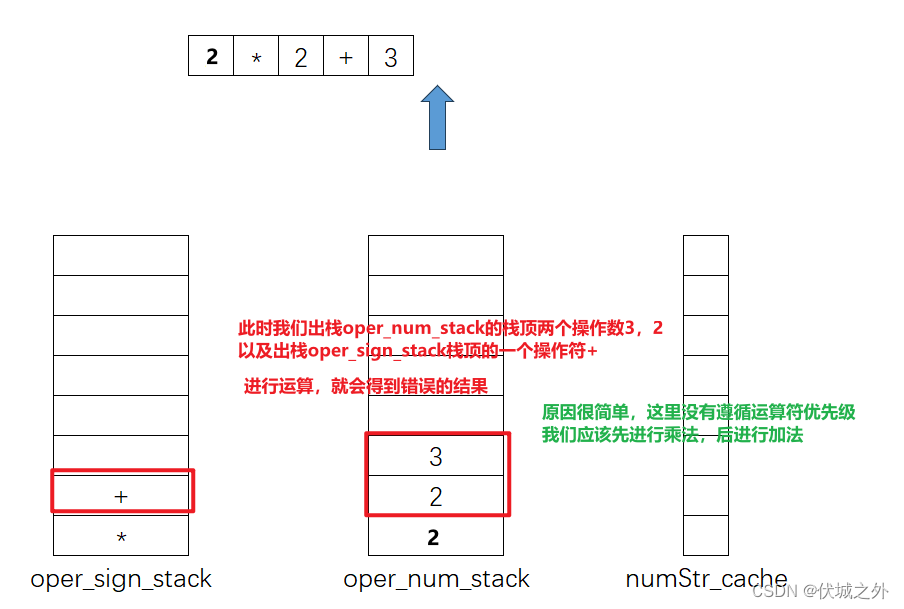
上面运算出错的问题就在于,当+入栈oper_sign_stack前,我们应该比较要入栈的'+'运算,和栈顶的'*'运算,哪个优先级更高,如果栈顶运算符优先级更高,此时我们应该先将栈顶运算符出栈运算,即如下:
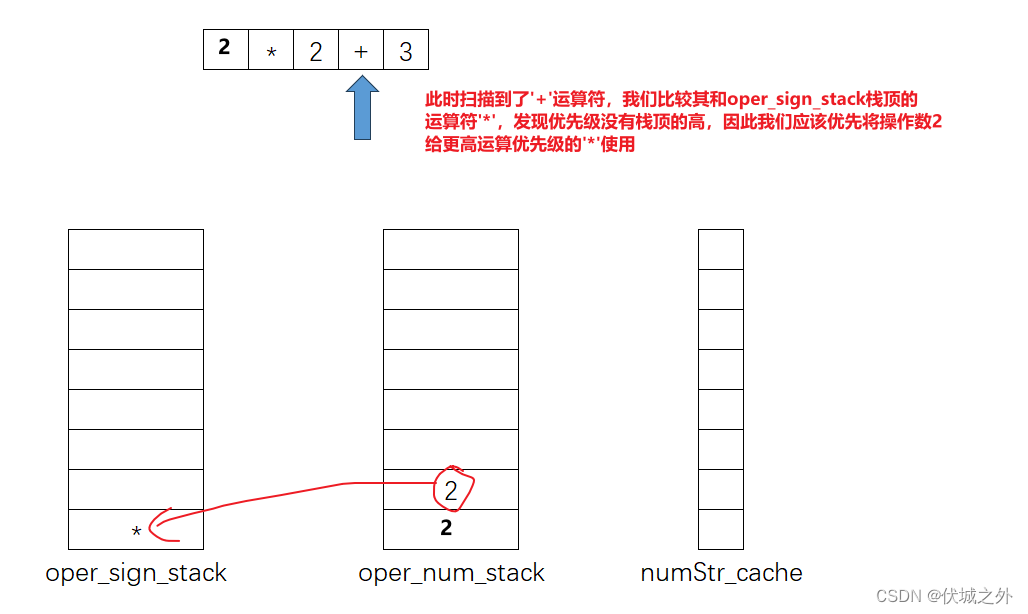
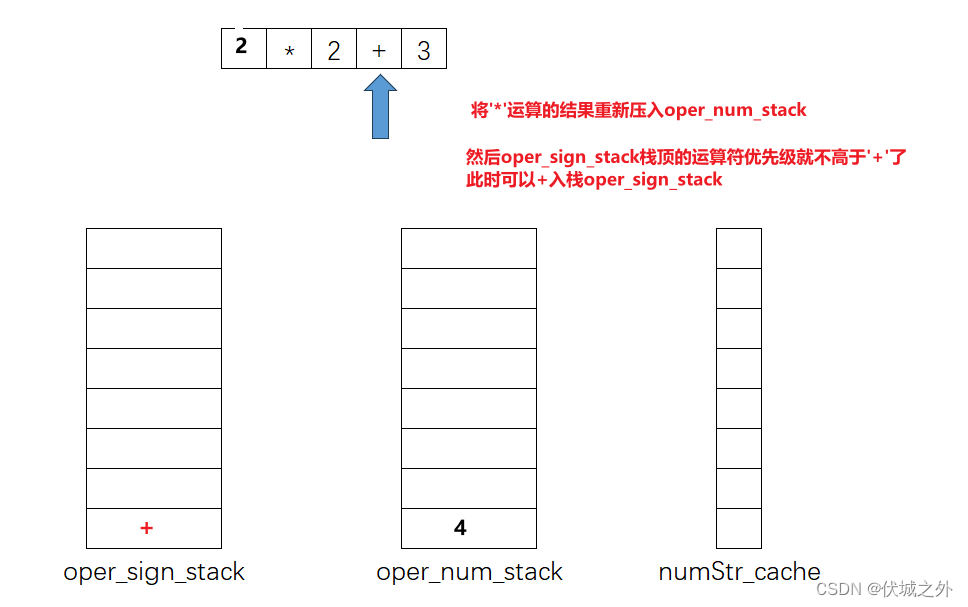
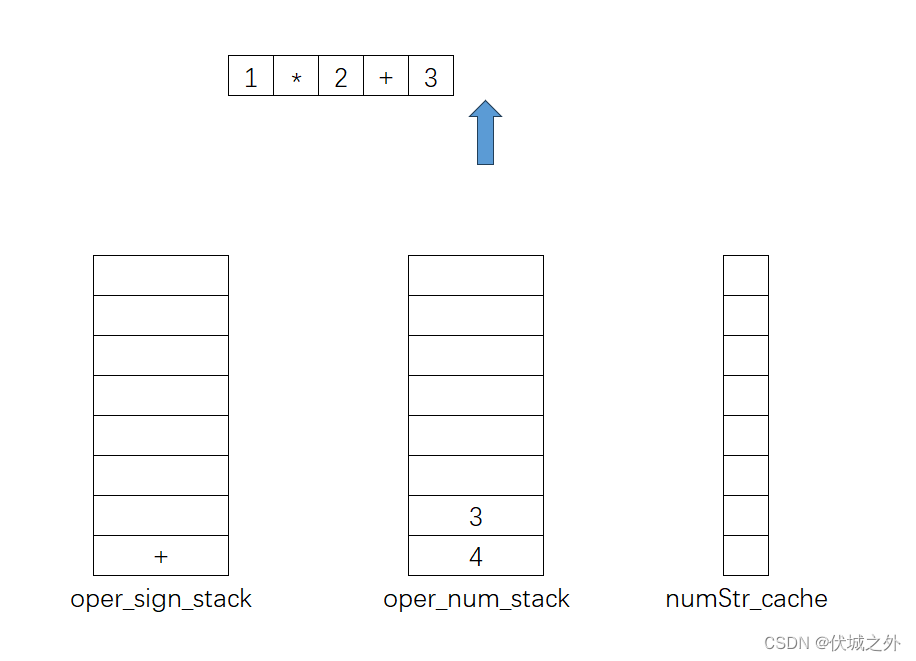
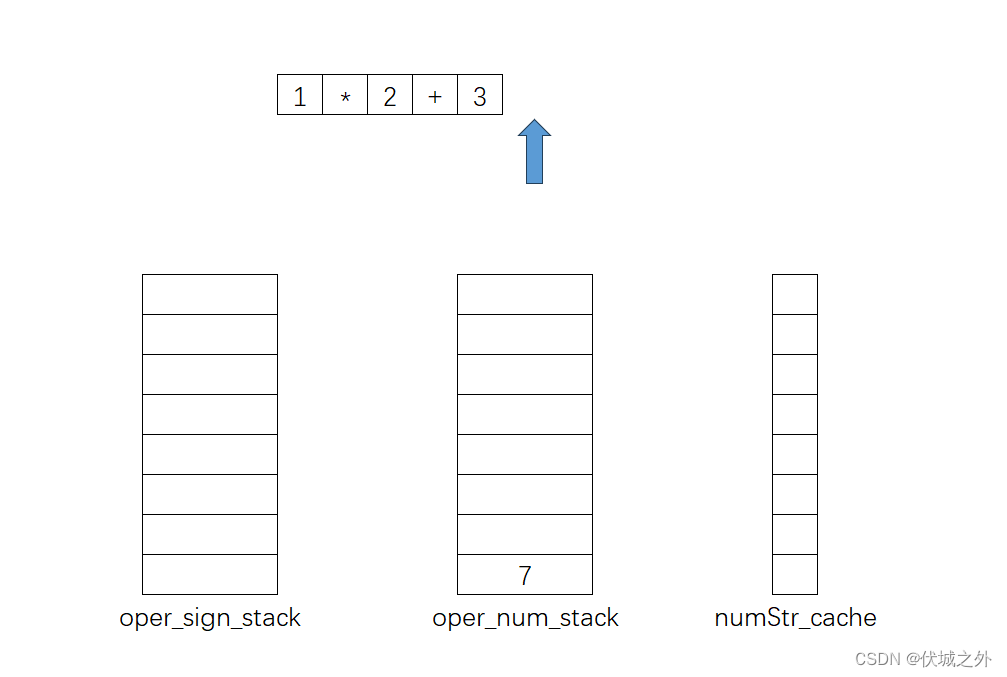
另外,对于运算符入栈时,对比oper_sign_stack栈顶的运算符,如果二者优先级一样,则也需要将oper_sign_stack栈顶运算先出栈运算。
且只要oper_sign_stack栈顶的运算符 的优先级>= 需要入栈的运算符,则oper_sign_stack就需要不停的出栈运算。
因此,总结一下就是,如果扫描到了运算符,此时需要和oper_sign_stack栈顶的运算符比较优先级,如果栈顶运算符优先级 >= 当前扫描运算符,则栈顶运算符需要出栈运算,直到oper_sign_stack栈顶运算符优先级小于当前扫描运算符。
另外,本题表达式中还可能出现(),那么遇到括号该怎么处理呢?
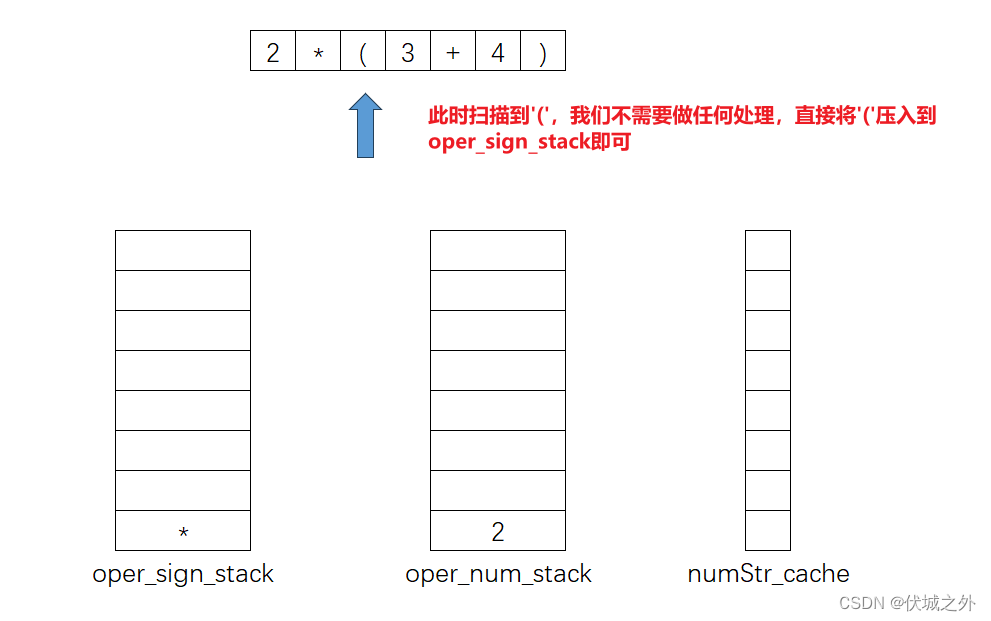
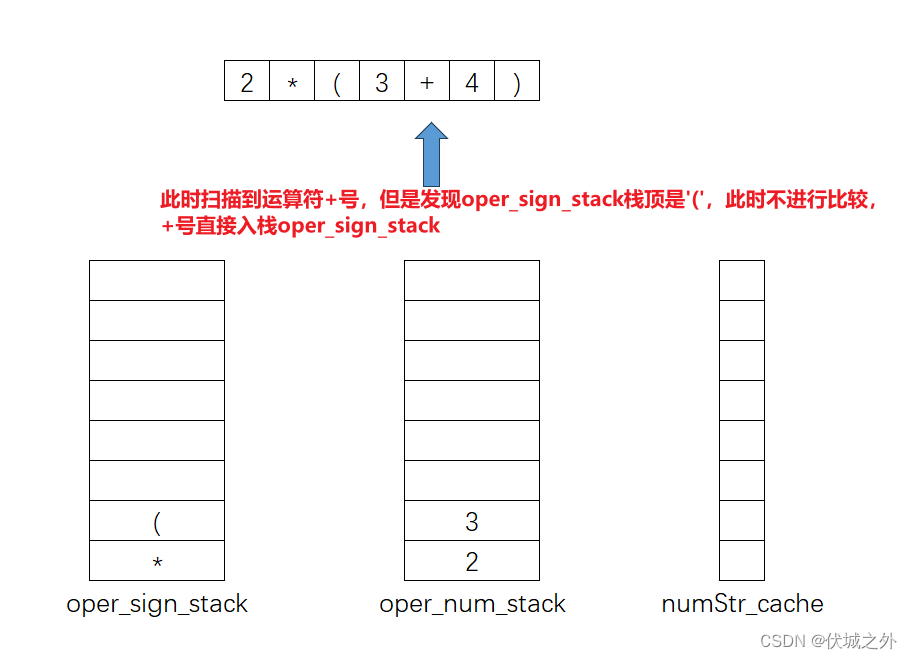
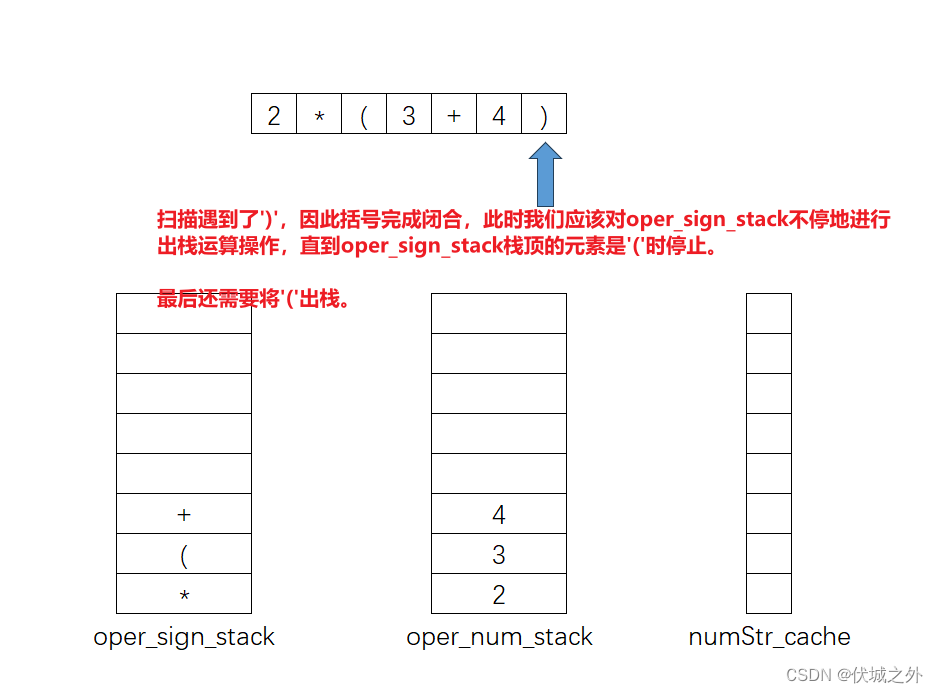
也就是说:
'(' 对于 +-*/ 运算的入栈oper_sign_stack的逻辑不产生影响,仅用于扫描到')'时oper_sign_stack的出栈结束界定。
需要注意的时,()内的+-*/运算依旧按照之前的逻辑入栈oper_sign_stack。
以上就是中缀表达式的基于双栈的解题思路。更具体的逻辑,请看代码实现。
分数的四则运算
本题还对中缀表达式计算做了一些改动,即要求的除法不是整除,而是保留最简分数结果。
比如 1 / 2 + 3 / 4 的结果不是0,而是 5 / 4。
解决方案很简单,我们之前在 oper_num_stack 中记录的都是整数操作数,现在我们只要改为分数操作数即可。
但是编程语言中并不支持分数,因此我们可以将分数拆分为分子和分母两部分,进行记录。即可以定义一个类,有如下属性:
{
ch:, // 分子
fa:, // 分母
}
分数的分子和分母必然是整数。
如果入栈的元素是一个整数num,则将其转化为如下分数后入栈oper_num_stack
{
ch: num,
fa: 1,
}
当我们需要进行出栈运算时,取出的oper_num_stack栈顶的两个操作数,假设分别为a,b,则:
对于加法运算的结果为:
{
ch: a.ch * b.fa + b.ch * a.fa,
fa: a.fa * b.fa,
}
比如 a = 1 / 3, b = 3 / 4,进行加法运算时,我们应该将他们的分母变为一样,即同时转为 3 * 4
则 a = (1 * 4) / (3 * 4), b = (3 * 3)/ (4 * 3)
按照此逻辑,减法运算结果为:
{
ch: a.ch * b.fa – b.ch * a.fa,
fa: a.fa * b.fa,
}
而乘法运算结果:
{
ch: a.ch * b.ch,
fa: a.fa * b.fa,
}
除法运算结果为:
{
ch: a.ch * b.fa,
fa: a.fa * b.ch,
}
这样的话,我们就完成了分数的四则运算。
分数的最简格式转化
最后就是关于,分数的最简格式转化了,其实也很简单,就是将分子、分母的最大公约数求解出来,然后分子、分母同时除以最大公约数,即可得到最简格式的分数。
而两个数的最大公约数的求解,可以使用辗转相除法。如果不熟悉辗转相除法,可以去网上搜索相关资料。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
// 输入输出处理
void (async function () {
console.log(getResult(await readline()));
})();
// 分数
class Fractions {
constructor(fa, ch) {
this.fa = fa; // 分母
this.ch = ch; // 分子
}
}
// 操作数栈
const oper_num = [];
// 操作符栈
const oper_sign = [];
function getResult(s) {
// +,-,*,/ 运算符优先级
const priority = {
"+": 1,
"-": 1,
"*": 2,
"/": 2,
};
// 操作数的字符缓存容器
let numStr = [];
let i = 0;
while (i < s.length) {
let c = s[i];
// 遇到数字字符
if (c >= "0" && c <= "9") {
// 则将该数字所在操作数的剩余数字字符一次性探索完
while (c >= "0" && c <= "9") {
numStr.push(c);
if (i + 1 >= s.length) break;
i++;
c = s[i];
}
// 探索完后,将操作数缓存容器中记录的字符,变为分数后,压入操作数栈
oper_num.push(new Fractions(1, parseInt(numStr.join(""))));
// 注意清空操作数缓存容器
numStr.length = 0;
}
// 遇到运算符
if (c == "+" || c == "-" || c == "*" || c == "/") {
// 只要栈顶运算符的优先级 >= 当前运算符,就需要不停出栈运算
while (
oper_sign.length > 0 &&
oper_sign.at(-1) != "(" &&
priority[c] <= priority[oper_sign.at(-1)]
) {
calc();
}
oper_sign.push(c);
} else if (c == ")") {
// 遇到')', 需要将操作符栈中靠近栈顶的'('后面的运算都出栈做了
while (oper_sign.at(-1) != "(") {
calc();
}
// 最后将')'对应的'('出栈
oper_sign.pop();
} else if (c == "(") {
// 遇到'(',则直接压倒操作符栈
oper_sign.push(c);
}
i++;
}
// oper_num栈中还有2个以上的数,则还需要进行运算
while (oper_num.length > 1) {
calc();
}
// oper_num栈中只剩一个数时,该数就是表达式结果
const result = oper_num.pop();
// 如果结果的分母为0(除数为0),则不合法
if (result.fa == 0) {
return "ERROR";
}
// 求分子、分母的最大公约数,并进行约份,求得最简格式的分子,分母
const k = getMaxCommonDivisor(result.fa, result.ch);
result.fa /= k;
result.ch /= k;
// 求计算结果的符号,这里用乘法是为了避免 分母小,分子大,除法结果为0的情况,这样会丢失符号信息
const sign = result.fa * result.ch < 0 ? "-" : "";
const fa = Math.abs(result.fa);
const ch = Math.abs(result.ch);
if (fa == 1) {
// 如果分母为1,则直接输出分子
return sign + ch;
} else {
// 如果分母不为1,则输出 分子 / 分母
return sign + ch + "/" + fa;
}
}
// 取出oper_num栈顶两个操作数进行运算
function calc() {
// 操作数顺序会对运算产生影响
const b = oper_num.pop(); // 栈顶元素是运算符右边的操作数
const a = oper_num.pop(); // 栈顶倒数第二个元素是运算符左边的操作数
// 运算符
const op = oper_sign.pop();
// 记录运算结果
const result = new Fractions();
switch (op) {
case "+":
result.fa = a.fa * b.fa;
result.ch = a.ch * b.fa + b.ch * a.fa;
break;
case "-":
result.fa = a.fa * b.fa;
result.ch = a.ch * b.fa - b.ch * a.fa;
break;
case "*":
result.fa = a.fa * b.fa;
result.ch = a.ch * b.ch;
break;
case "/":
result.fa = a.fa * b.ch;
result.ch = a.ch * b.fa;
break;
}
oper_num.push(result);
}
// 辗转相除法,求两个数的最大公约数
function getMaxCommonDivisor(x, y) {
while (y != 0) {
let tmp = y;
y = x % y;
x = tmp;
}
return x;
}
Java算法源码
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
// 分数
static class Fractions {
int fa; // 分母
int ch; // 分子
public Fractions() {}
public Fractions(int fa, int ch) {
this.fa = fa;
this.ch = ch;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(getResult(sc.nextLine()));
}
// 操作数栈
static LinkedList<Fractions> oper_num = new LinkedList<>();
// 操作符栈
static LinkedList<Character> oper_sign = new LinkedList<>();
public static String getResult(String s) {
// +,-,*,/ 运算符优先级
HashMap<Character, Integer> priority = new HashMap<>();
priority.put('+', 1);
priority.put('-', 1);
priority.put('*', 2);
priority.put('/', 2);
// 操作数的字符缓存容器
StringBuilder numStr = new StringBuilder();
int i = 0;
while (i < s.length()) {
char c = s.charAt(i);
// 遇到数字字符
if (c >= '0' && c <= '9') {
// 则将该数字所在操作数的剩余数字字符一次性探索完
while (c >= '0' && c <= '9') {
numStr.append(c);
if (i + 1 >= s.length()) break;
i++;
c = s.charAt(i);
}
// 探索完后,将操作数缓存容器中记录的字符,变为分数后,压入操作数栈
oper_num.addLast(new Fractions(1, Integer.parseInt(numStr.toString())));
// 注意清空操作数缓存容器
numStr = new StringBuilder();
}
// 遇到运算符
if (c == '+' || c == '-' || c == '*' || c == '/') {
// 只要栈顶运算符的优先级 >= 当前运算符,就需要不停出栈运算
while (oper_sign.size() > 0
&& oper_sign.getLast() != '('
&& priority.get(c) <= priority.get(oper_sign.getLast())) {
calc();
}
oper_sign.addLast(c);
} else if (c == ')') {
// 遇到')', 需要将操作符栈中靠近栈顶的'('后面的运算都出栈做了
while (oper_sign.getLast() != '(') {
calc();
}
// 最后将')'对应的'('出栈
oper_sign.removeLast();
} else if (c == '(') {
// 遇到'(',则直接压倒操作符栈
oper_sign.add(c);
}
i++;
}
// oper_num栈中还有2个以上的数,则还需要进行运算
while (oper_num.size() > 1) {
calc();
}
// oper_num栈中只剩一个数时,该数就是表达式结果
Fractions result = oper_num.removeLast();
// 如果结果的分母为0(除数为0),则不合法
if (result.fa == 0) {
return "ERROR";
}
// 求分子、分母的最大公约数,并进行约份,求得最简格式的分子,分母
int k = getMaxCommonDivisor(result.fa, result.ch);
result.fa /= k;
result.ch /= k;
// 求计算结果的符号,这里用乘法是为了避免 分母小,分子大,除法结果为0的情况,这样会丢失符号信息
String sign = result.fa * result.ch < 0 ? "-" : "";
int fa = Math.abs(result.fa);
int ch = Math.abs(result.ch);
if (fa == 1) {
// 如果分母为1,则直接输出分子
return sign + ch;
} else {
// 如果分母不为1,则输出 分子 / 分母
return sign + ch + "/" + fa;
}
}
// 取出oper_num栈顶两个操作数进行运算
public static void calc() {
// 操作数顺序会对运算产生影响
Fractions b = oper_num.removeLast(); // 栈顶元素是运算符右边的操作数
Fractions a = oper_num.removeLast(); // 栈顶倒数第二个元素是运算符左边的操作数
// 运算符
char op = oper_sign.removeLast();
// 记录运算结果
Fractions result = new Fractions();
switch (op) {
case '+':
result.fa = a.fa * b.fa;
result.ch = a.ch * b.fa + b.ch * a.fa;
break;
case '-':
result.fa = a.fa * b.fa;
result.ch = a.ch * b.fa - b.ch * a.fa;
break;
case '*':
result.fa = a.fa * b.fa;
result.ch = a.ch * b.ch;
break;
case '/':
result.fa = a.fa * b.ch;
result.ch = a.ch * b.fa;
break;
}
oper_num.add(result);
}
// 辗转相除法,求两个数的最大公约数
public static int getMaxCommonDivisor(int x, int y) {
while (y != 0) {
int tmp = y;
y = x % y;
x = tmp;
}
return x;
}
}
Python算法源码
# 输入获取
s = input()
# 操作数栈
oper_num = []
# 操作符栈
oper_sign = []
# 分数类
class Fractions:
def __init__(self, fa, ch):
self.fa = fa # 分母
self.ch = ch # 分子
# 辗转相除法,求两个数的最大公约数
def getMaxCommonDivisor(x, y):
while y != 0:
tmp = y
y = x % y
x = tmp
return x
# 取出oper_num栈顶两个操作数进行运算
def calc():
# 操作数顺序会对运算产生影响
b = oper_num.pop() # 栈顶元素是运算符右边的操作数
a = oper_num.pop() # 栈顶倒数第二个元素是运算符左边的操作数
# 运算符
op = oper_sign.pop()
# 记录运算结果
result = Fractions(None, None)
if op == '+':
result.fa = a.fa * b.fa
result.ch = a.ch * b.fa + b.ch * a.fa
elif op == '-':
result.fa = a.fa * b.fa
result.ch = a.ch * b.fa - b.ch * a.fa
elif op == '*':
result.fa = a.fa * b.fa
result.ch = a.ch * b.ch
elif op == '/':
result.fa = a.fa * b.ch
result.ch = a.ch * b.fa
oper_num.append(result)
def getResult():
# +,-,*,/ 运算符优先级
priority = {
"+": 1,
"-": 1,
"*": 2,
"/": 2
}
# 操作数的字符缓存容器
numStr = []
i = 0
while i < len(s):
c = s[i]
# 遇到数字字符
if '9' >= c >= '0':
# 则将该数字所在操作数的剩余数字字符一次性探索完
while '9' >= c >= '0':
numStr.append(c)
if i + 1 >= len(s):
break
i += 1
c = s[i]
# 探索完后,将操作数缓存容器中记录的字符,变为分数后,压入操作数栈
oper_num.append(Fractions(1, int("".join(numStr))))
# 注意清空操作数缓存容器
numStr.clear()
# 遇到运算符
if c == '+' or c == '-' or c == '*' or c == '/':
# 只要栈顶运算符的优先级 >= 当前运算符,就需要不停出栈运算
while len(oper_sign) > 0 and oper_sign[-1] != '(' and priority[c] <= priority[oper_sign[-1]]:
calc()
oper_sign.append(c)
elif c == ')':
# 遇到')', 需要将操作符栈中靠近栈顶的'('后面的运算都出栈做了
while oper_sign[-1] != '(':
calc()
# 最后将')'对应的'('出栈
oper_sign.pop()
elif c == '(':
# 遇到'(',则直接压倒操作符栈
oper_sign.append(c)
i += 1
# oper_num栈中还有2个以上的数,则还需要进行运算
while len(oper_num) > 1:
calc()
# oper_num栈中只剩一个数时,该数就是表达式结果
result = oper_num.pop()
# 如果结果的分母为0(除数为0),则不合法
if result.fa == 0:
return "ERROR"
# 求分子、分母的最大公约数,并进行约份,求得最简格式的分子,分母
k = getMaxCommonDivisor(result.fa, result.ch)
result.fa //= k
result.ch //= k
# 求计算结果的符号,这里用乘法是为了避免 分母小,分子大,除法结果为0的情况,这样会丢失符号信息
sign = "-" if result.fa * result.ch < 0 else ""
fa = abs(result.fa)
ch = abs(result.ch)
if fa == 1:
# 如果分母为1,则直接输出分子
return f"{sign}{ch}"
else:
# 如果分母不为1,则输出 分子 / 分母
return f"{sign}{ch}/{fa}"
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_LENGTH 200
// 分数结构
typedef struct Fractions {
int fa; // 分母
int ch; // 分子
} Fractions;
Fractions *new_Fractions(int fa, int ch) {
Fractions *fra = (Fractions *) malloc(sizeof(Fractions));
fra->fa = fa;
fra->ch = ch;
return fra;
}
// 操作数栈
Fractions *oper_num[MAX_LENGTH];
int oper_num_size = 0;
// 操作符栈
char oper_sign[MAX_LENGTH];
int oper_sign_size = 0;
// 辗转相除法,求两个数的最大公约数
int getMaxCommonDivisor(int x, int y) {
while (y != 0) {
int tmp = y;
y = x % y;
x = tmp;
}
return x;
}
// 取出oper_num栈顶两个操作数进行运算
void calc() {
// 操作数顺序会对运算产生影响
Fractions *b = oper_num[--oper_num_size]; // 栈顶元素是运算符右边的操作数
Fractions *a = oper_num[--oper_num_size]; // 栈顶倒数第二个元素是运算符左边的操作数
// 运算符
char op = oper_sign[--oper_sign_size];
// 记录运算结果
Fractions *result = new_Fractions(1, 0);
if (op == '+') {
result->fa = a->fa * b->fa;
result->ch = a->ch * b->fa + b->ch * a->fa;
} else if (op == '-') {
result->fa = a->fa * b->fa;
result->ch = a->ch * b->fa - b->ch * a->fa;
} else if (op == '*') {
result->fa = a->fa * b->fa;
result->ch = a->ch * b->ch;
} else if (op == '/') {
result->fa = a->fa * b->ch;
result->ch = a->ch * b->fa;
}
oper_num[oper_num_size++] = result;
}
int main() {
char s[MAX_LENGTH];
gets(s);
// +,-,*,/ 运算符优先级
int priority[128] = {0};
priority['+'] = 1;
priority['-'] = 1;
priority['*'] = 2;
priority['/'] = 2;
// 操作数的字符缓存容器
char numStr[MAX_LENGTH] = {'�'};
int numStr_size = 0;
int i = 0;
while (s[i] != '�') {
char c = s[i];
// 遇到数字字符
if (c >= '0' && c <= '9') {
// 则将该数字所在操作数的剩余数字字符一次性探索完
while (c >= '0' && c <= '9') {
numStr[numStr_size++] = c;
if (s[i + 1] == '�') break;
i++;
c = s[i];
}
// 探索完后,将操作数缓存容器中记录的字符,变为分数后,压入操作数栈
oper_num[oper_num_size++] = new_Fractions(1, atoi(numStr));
// 注意清空操作数缓存容器
memset(numStr, '�', MAX_LENGTH);
numStr_size = 0;
}
// 遇到运算符
if (c == '+' || c == '-' || c == '*' || c == '/') {
// 只要栈顶运算符的优先级 >= 当前运算符,就需要不停出栈运算
while (oper_sign_size > 0 && oper_sign[oper_sign_size - 1] != '(' &&
priority[c] <= priority[oper_sign[oper_sign_size - 1]]) {
calc();
}
oper_sign[oper_sign_size++] = c;
} else if (c == ')') {
// 遇到')', 需要将操作符栈中靠近栈顶的'('后面的运算都出栈做了
while (oper_sign[oper_sign_size - 1] != '(') {
calc();
}
// 最后将')'对应的'('出栈
oper_sign_size--;
} else if (c == '(') {
// 遇到'(',则直接压倒操作符栈
oper_sign[oper_sign_size++] = c;
}
i++;
}
// oper_num栈中还有2个以上的数,则还需要进行运算
while (oper_num_size > 1) {
calc();
}
// oper_num栈中只剩一个数时,该数就是表达式结果
Fractions *result = oper_num[--oper_num_size];
// 如果结果的分母为0(除数为0),则不合法
if (result->fa == 0) {
puts("ERROR");
return 0;
}
// 求分子、分母的最大公约数,并进行约份,求得最简格式的分子,分母
int k = getMaxCommonDivisor(result->fa, result->ch);
result->fa /= k;
result->ch /= k;
// 求计算结果的符号,这里用乘法是为了避免 分母小,分子大,除法结果为0的情况,这样会丢失符号信息
if ((result->fa > 0 && result->ch < 0) || (result->ch > 0 && result->fa < 0)) {
printf("-");
}
int fa = abs(result->fa);
int ch = abs(result->ch);
if (fa == 1) {
// 如果分母为1,则直接输出分子
printf("%dn", ch);
} else {
// 如果分母不为1,则输出 分子 / 分母
printf("%d/%dn", ch, fa);
}
return 0;
}免责声明:
评论0