题目描述
某部门计划通过结队编程来进行项目开发,
已知该部门有 N 名员工,每个员工有独一无二的职级,每三个员工形成一个小组进行结队编程,结队分组规则如下:
从部门中选出序号分别为 i、j、k 的3名员工,他们的职级分贝为 level[i],level[j],level[k],
结队小组满足 level[i] < level[j] < level[k] 或者 level[i] > level[j] > level[k],
其中 0 ≤ i < j < k < n。
请你按上述条件计算可能组合的小组数量。同一员工可以参加多个小组。
输入描述
第一行输入:员工总数 n
第二行输入:按序号依次排列的员工的职级 level,中间用空格隔开
限制:
- 1 ≤ n ≤ 6000
- 1 ≤ level[i] ≤ 10^5
输出描述
可能结队的小组数量
用例
| 输入 | 4 1 2 3 4 |
| 输出 | 4 |
| 说明 | 可能结队成的组合(1,2,3)、(1,2,4)、(1,3,4)、(2,3,4) |
| 输入 | 3 5 4 7 |
| 输出 | 0 |
| 说明 | 根据结队条件,我们无法为该部门组建小组 |
题目解析
本题的意思其实就是让我们求解给定输入数组中,比如用例1中 [1,2,3,4] ,每个数组元素:
- 左边比自己大的元素的个数,设为:leftBiggerCount
- 左边比自己小的元素的个数,设为:leftSmallerCount
- 右边比自己大的元素的个数,设为:rightBiggerCount
- 右边比自己小的元素是的个数,设为:rightSmallerCount
当我们求解出每个数组元素的上述信息后,累加每个数组元素的如下计算结果:
leftBiggerCount * rightSmallerCount + leftSmallerCount * rightBiggerCount
比如题目用例1中,数组 [1,2,3,4],索引为 idx
- idx=0元素,leftBiggerCount = 0,leftSmallerCount = 0,rightBiggerCount = 3,rightSmallerCount = 0
leftBiggerCount * rightSmallerCount + leftSmallerCount * rightBiggerCount = 0
- idx=1元素,leftBiggerCount = 0,leftSmallerCount = 1,rightBiggerCount = 2,rightSmallerCount = 0
leftBiggerCount * rightSmallerCount + leftSmallerCount * rightBiggerCount = 2
- idx=2元素,leftBiggerCount = 0,leftSmallerCount = 2,rightBiggerCount = 1,rightSmallerCount = 0
leftBiggerCount * rightSmallerCount + leftSmallerCount * rightBiggerCount = 2
- idx=3元素,leftBiggerCount = 0,leftSmallerCount = 3,rightBiggerCount = 0,rightSmallerCount = 0
leftBiggerCount * rightSmallerCount + leftSmallerCount * rightBiggerCount = 0
因此数组[1,2,3,4]的结队编程数量为4。
暴力解法
那么如何求解每个元素左右两边大于自己,小于自己的元素数量呢?
最简单的思路是暴力求解。定义两层循环,外层确定结队中间值,内层两个平级循环,分别扫描中间值左边,和中间值右边。
整体时间复杂度O(n^2),本题1 ≤ n ≤ 6000,有超时的可能。
具体实现请看代码。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
// 输入处理
void (async function () {
const n = parseInt(await readline());
const levels = (await readline()).split(" ").map(Number);
console.log(getResult(n, levels));
})();
function getResult(n, levels) {
let ans = 0;
for (let i = 1; i < n - 1; i++) {
let mid = levels[i];
let leftSmallerCount = 0;
let leftBiggerCount = 0;
for (let j = 0; j < i; j++) {
if (levels[j] > mid) {
leftBiggerCount++;
} else {
leftSmallerCount++;
}
}
let rightSmallerCount = 0;
let rightBiggerCount = 0;
for (let k = i + 1; k < n; k++) {
if (levels[k] > mid) {
rightBiggerCount++;
} else {
rightSmallerCount++;
}
}
ans +=
leftBiggerCount * rightSmallerCount + leftSmallerCount * rightBiggerCount;
}
return ans;
}
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());
int[] levels = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
System.out.println(getResult(n, levels));
}
public static long getResult(int n, int[] levels) {
long ans = 0;
for (int i = 1; i < n - 1; i++) {
int mid = levels[i];
long leftSmallerCount = 0;
long leftBiggerCount = 0;
for (int j = 0; j < i; j++) {
if (levels[j] > mid) {
leftBiggerCount++;
} else {
leftSmallerCount++;
}
}
long rightSmallerCount = 0;
long rightBiggerCount = 0;
for (int k = i + 1; k < n; k++) {
if (levels[k] > mid) {
rightBiggerCount++;
} else {
rightSmallerCount++;
}
}
ans += leftSmallerCount * rightBiggerCount + leftBiggerCount * rightSmallerCount;
}
return ans;
}
}
Python算法源码
# 输入获取
n = int(input())
levels = list(map(int, input().split()))
# 算法入口
def getResult():
ans = 0
for i in range(1, n - 1):
mid = levels[i]
leftSmallerCount = 0
leftBiggerCount = 0
for j in range(i):
if levels[j] > mid:
leftBiggerCount += 1
else:
leftSmallerCount += 1
rightSmallerCount = 0
rightBiggerCount = 0
for k in range(i + 1, n):
if levels[k] > mid:
rightBiggerCount += 1
else:
rightSmallerCount += 1
ans += leftSmallerCount * rightBiggerCount + leftBiggerCount * rightSmallerCount
return ans
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 6000
int main() {
int n;
scanf("%d", &n);
int levels[MAX_SIZE];
int levels_size = 0;
while (scanf("%d", &levels[levels_size++])) {
if (getchar() != ' ') break;
}
long ans = 0;
for (int i = 1; i < n - 1; i++) {
int mid = levels[i];
long leftSmallerCount = 0;
long leftBiggerCount = 0;
for (int j = 0; j < i; j++) {
if (levels[j] > mid) {
leftBiggerCount++;
} else {
leftSmallerCount++;
}
}
long rightSmallerCount = 0;
long rightBiggerCount = 0;
for (int k = i + 1; k < n; k++) {
if (levels[k] > mid) {
rightBiggerCount++;
} else {
rightSmallerCount++;
}
}
ans += leftSmallerCount * rightBiggerCount + leftBiggerCount * rightSmallerCount;
}
printf("%ldn", ans);
return 0;
}二叉搜索树解法
本题更优策略可以使用二叉搜索树,将时间复杂度降到O(NlogN)。
二叉搜索树,也叫二叉排序树,特点是其中序遍历序列是有序的。而构建二叉搜索树的步骤很简单,每次向二叉搜索树加入新节点时,都去和遇到的(子树)根节点进行比较:
- 如果 新节点的值 < 根节点的值,则插入到根节点的左子树中,然后继续递归和左子树根比较
- 如果 新节点的值 > 根节点的值,则插入到根节点的右子树中,然后继续递归和右子树根比较
因此,二叉搜索树中每个节点的左子树中所有节点的值都比自己小,右子树中所有节点的值都比自己大。
那么如何利用二叉搜索树解决本题呢?这里我通过图示说明。
首先我们来定义出二叉搜索树节点结构:
{
idx:, // 数组元素的索引
val:, // 当前节点值(数组元素的值)
left:, // 当前节点的左子节点
right:, // 当前节点的右子节点
rightSmallerCount:, // 该数组元素右边比自己小的元素的个数
leftChildCount:, // 该节点的左子树中节点个数
}
这里的二叉搜索树节点和数组元素是互相关联的。
然后,我们需要按照输入数组的倒序取元素插入到二叉搜索树中(PS:原因后面说明)
由于题目用例太极端,这里我自己建一个 [3, 1, 7, 2, 8, 6, 4 , 9, 5]
[3, 1, 7, 2, 8, 6, 4 , 9, 5]
插入5

[3, 1, 7, 2, 8, 6, 4 , 9, 5]
插入9

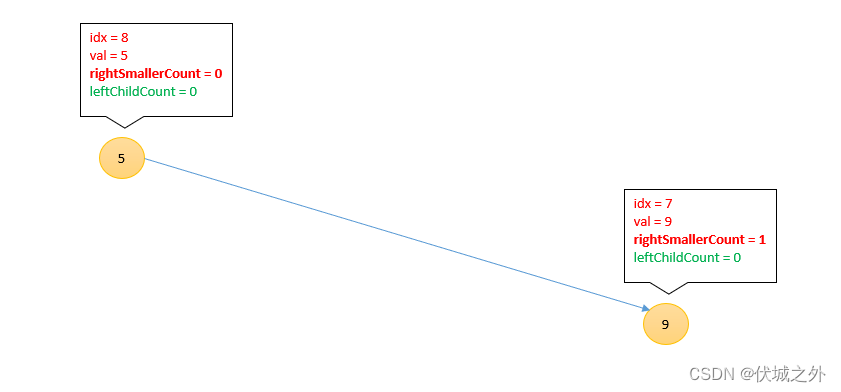
[3, 1, 7, 2, 8, 6, 4, 9, 5]
插入4
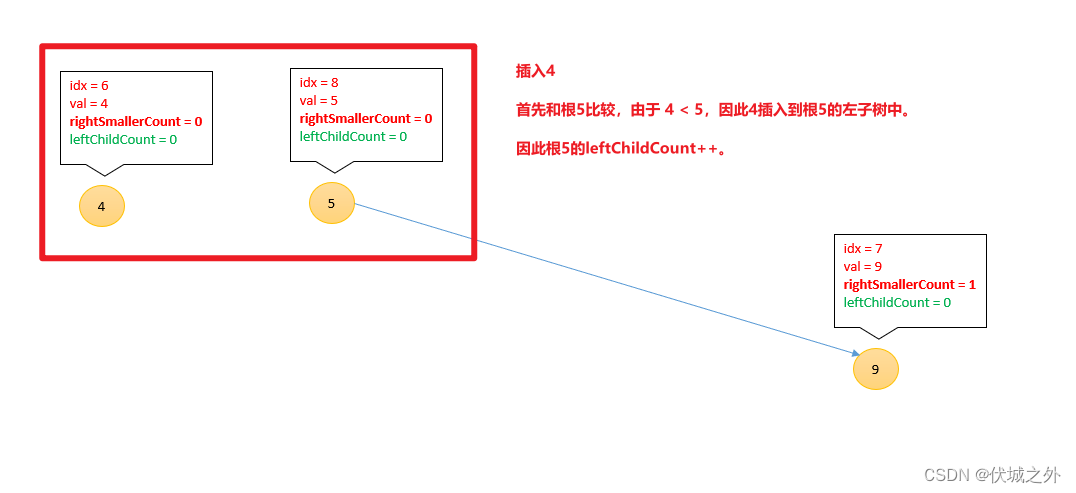
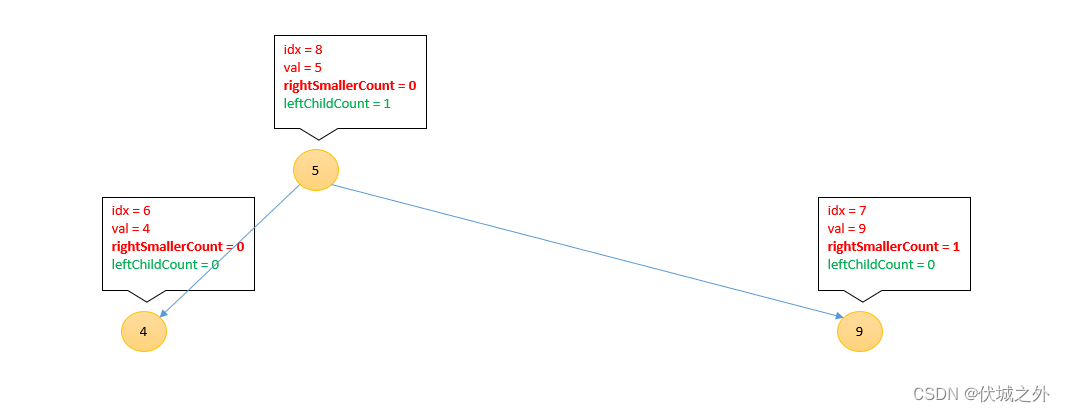
[3, 1, 7, 2, 8, 6, 4 , 9, 5]
插入6
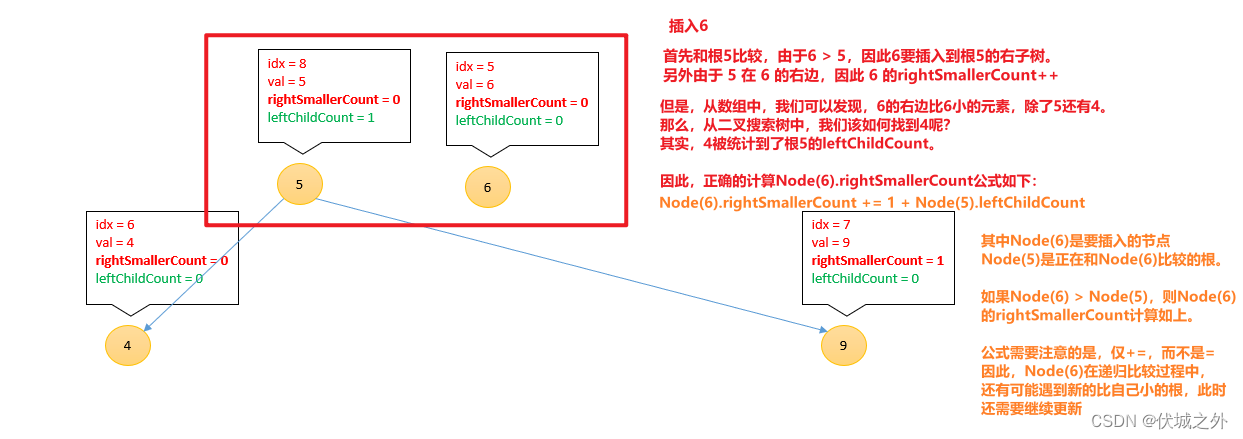
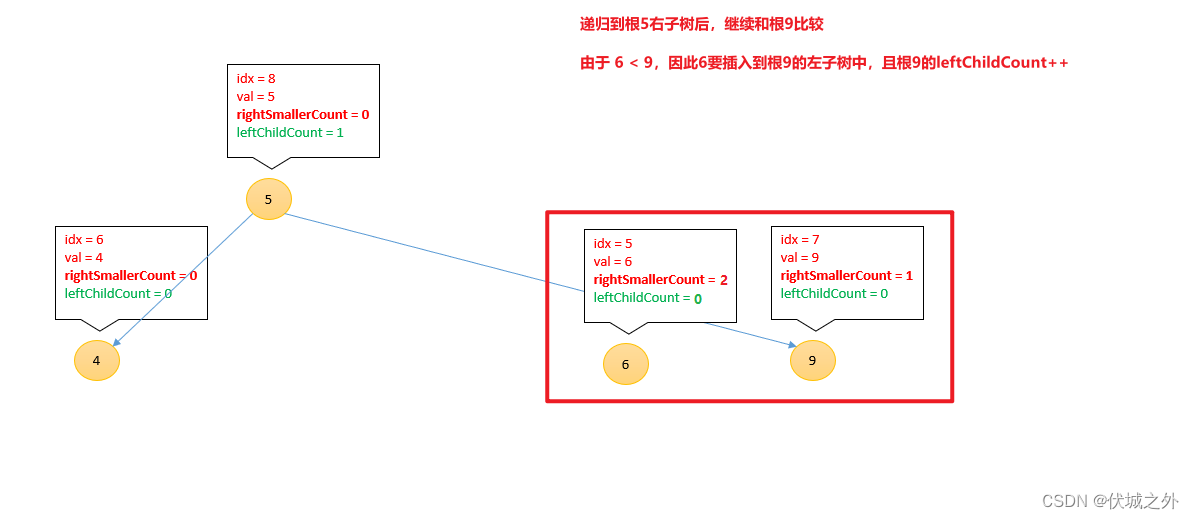
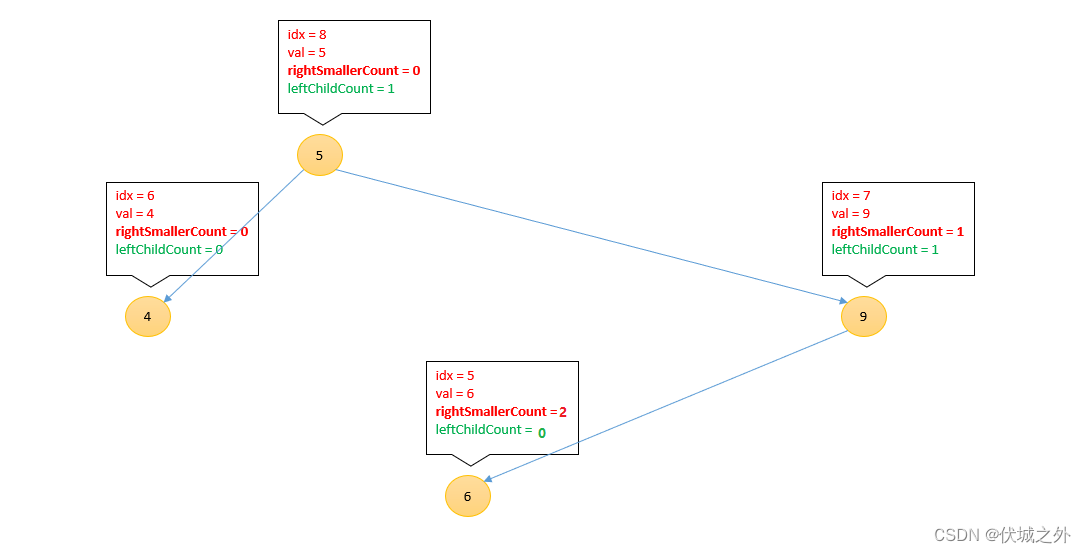
[3, 1, 7, 2, 8, 6, 4 , 9, 5]
插入8
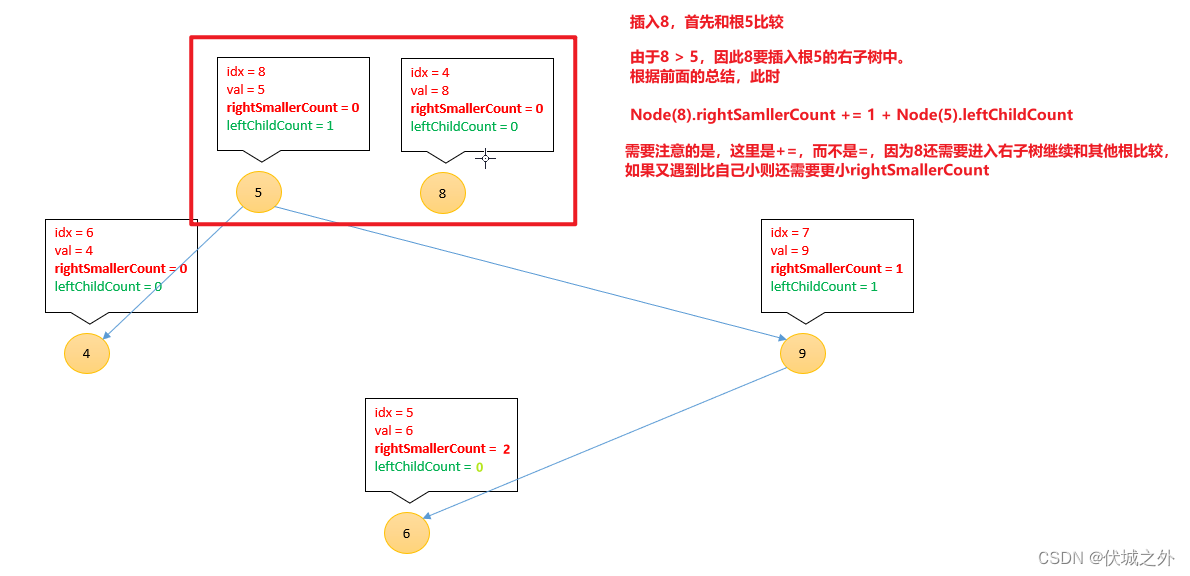
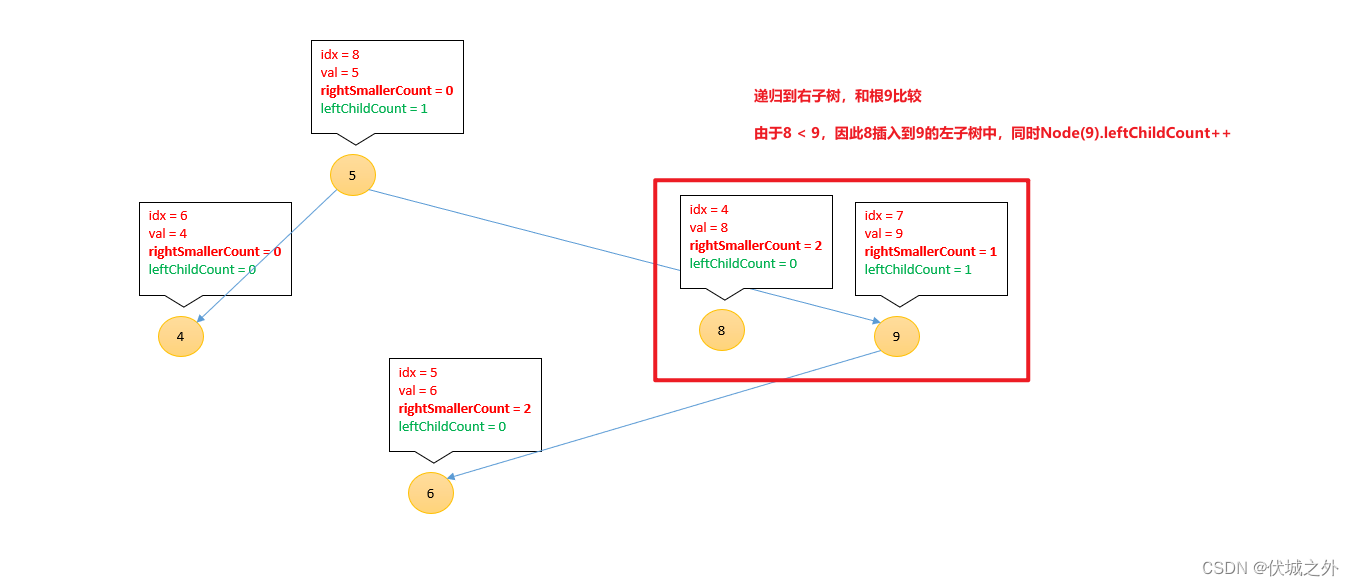
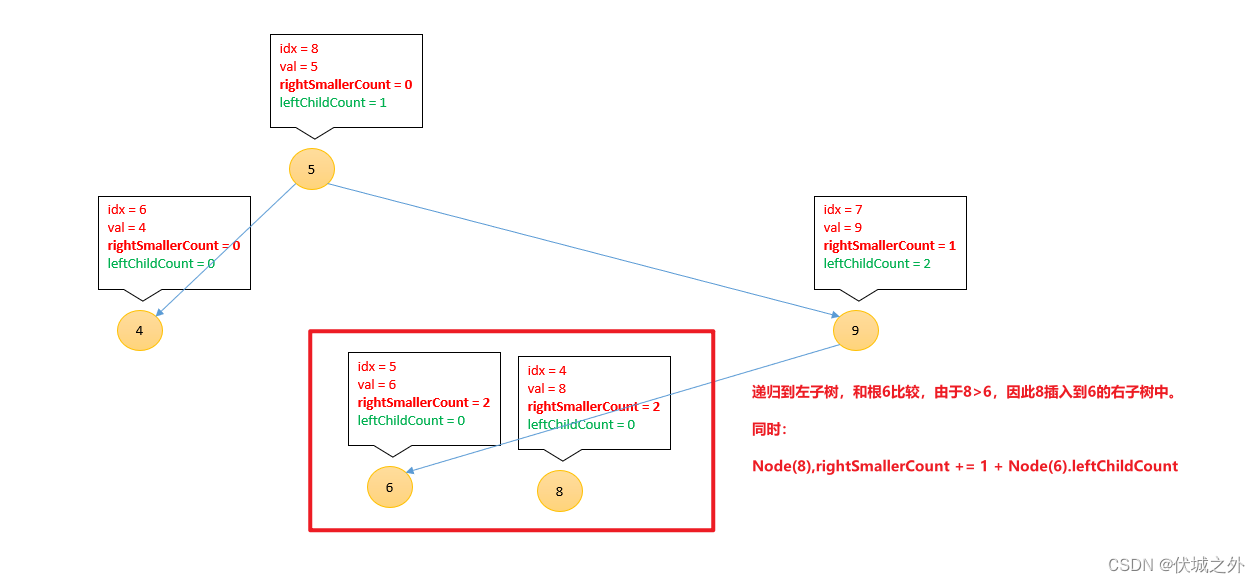
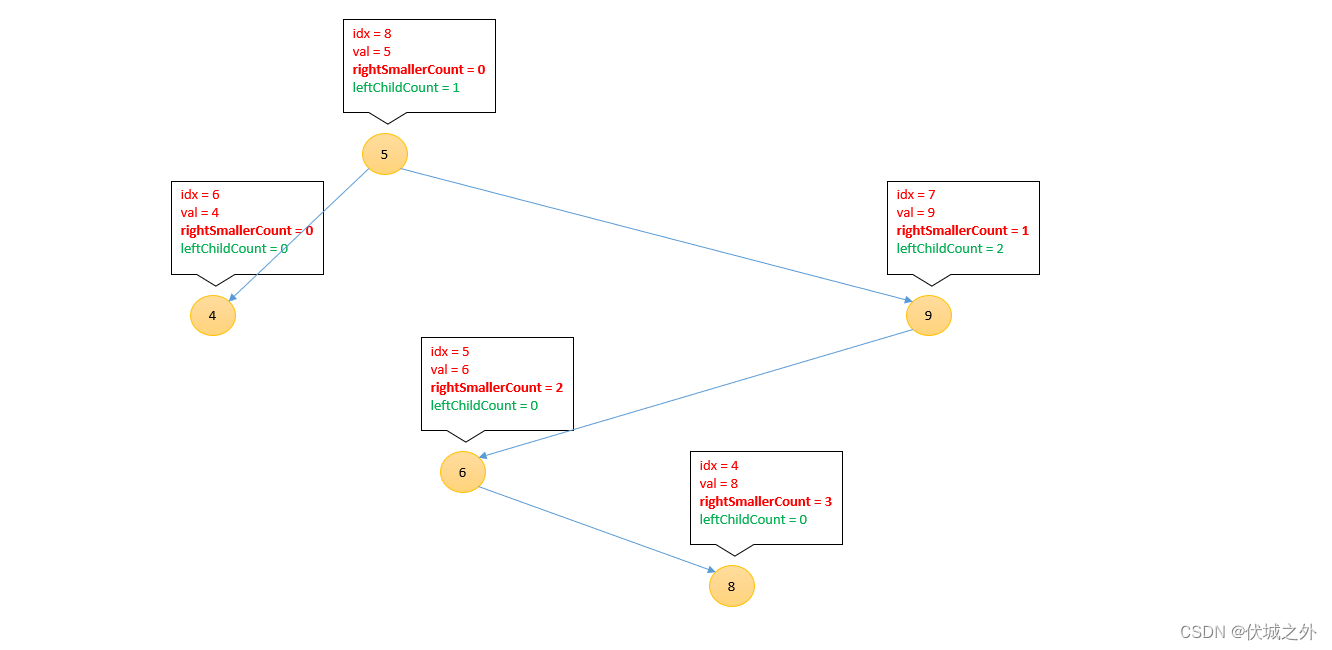
[3, 1, 7, 2, 8, 6, 4 , 9, 5]
插入2
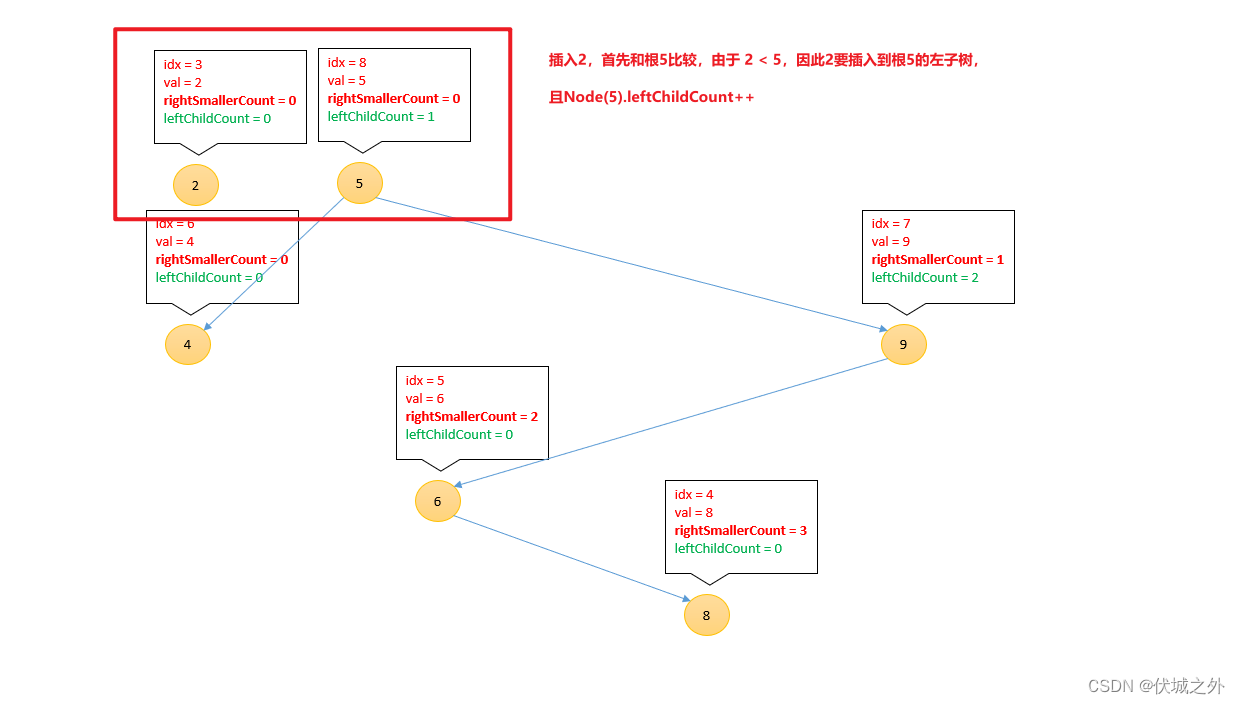
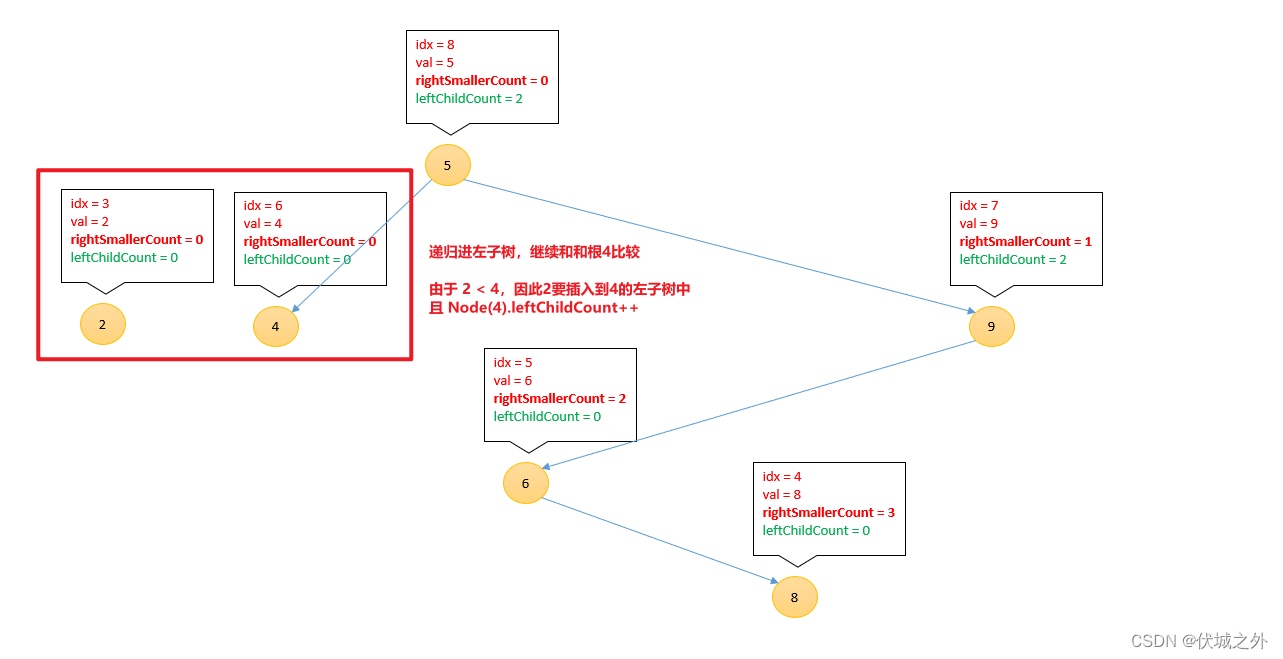
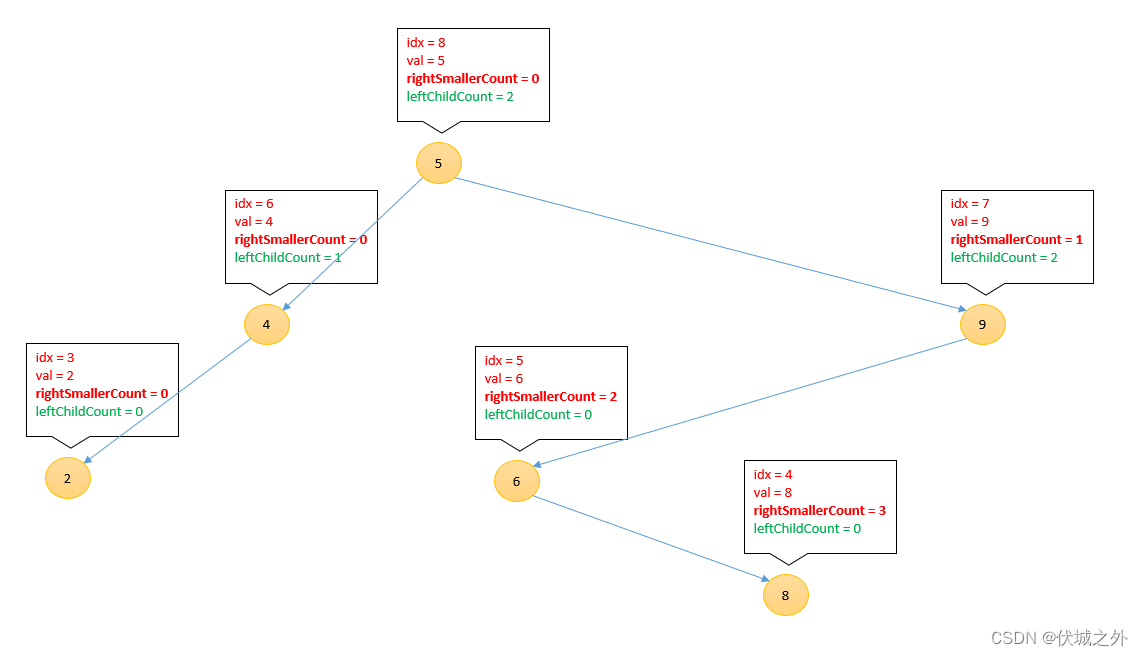
后面就不画了,大家可以自己继续往下推导。
总结一下,插入新节点到二叉搜索树中,新节点需要不断和各种子树的根进行比较:
- 如果新节点的值 < 根节点的值,则
Node(根).leftChildCount++
新节点递归进入根的左子树,继续比较
- 如果新节点的值 > 根节点的值,则
Node(新).rightSmallerCount += 1 + Node(根).leftChildCount
新节点递归进入根的右子树,继续比较
这样的话,当我们插入数组中所有元素后,每个节点上的rightSmallerCount即为对应元素:右边比自己小的元素的个数。
然后我们将原数组反转后,继续一遍上面构建二叉树的过程,即可得到数组中每个元素左边比自己小的元素的个数。(具体请看代码实现)
即,通过构建两个二叉搜索树,我们即可得到每个元素的:
- 左边比自己小的元素的个数 leftSmallerCount
- 右边比自己小的元素的个数 rightSmallerCount
而基于每个元素的索引位值idx,我们又能得到每个元素levels[idx]:
- 左边一共有多少个元素,levels[idx]左边一共idx个元素
- 右边一共有多少个元素,levels[idx]右边一共levels.length – 1 – idx个元素
那么每个元素的:
- 左边比自己大的元素的个数 leftBiggerCount = idx – leftSmallerCount
- 右边比自己大的元素的个数 rightBiggerCount = levels.length – 1 – idx – rightSmallerCount
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
// 输入处理
void (async function () {
const n = parseInt(await readline());
const levels = (await readline()).split(" ").map(Number);
console.log(getResult(n, levels));
})();
class Node {
constructor(idx, val) {
this.idx = idx; // 当前节点的值在原数组中的索引
this.val = val; // 当前节点的值
this.left = null; // 当前节点的左子节点
this.right = null; // 当前节点的右子节点
this.count = 0; // 当前节点的左子树中节点数量
}
}
/**
* 向二叉搜索树中插入新节点
*
* @param root (树/子树)根节点
* @param node 要插入的新节点
* @param res 数组,其中res[i]代表第i个节点右边比自己小的元素的个数
* @return 根节点
*/
function insertNode(root, node, res) {
if (root == null) {
return node;
}
// 由于本题中每个员工有独一无二的职级,即levels中所有元素值都不互相相同,因此这里非大即小
if (node.val < root.val) {
// 如果要插入的新节点的值,比根节点小,则插入根节点左子树
root.count++; // 根节点左子树的节点树+1
root.left = insertNode(root.left, node, res); // 递归进入左子树继续比较
} else {
// 如果要插入的新节点的值,比根节点大,则需要插入根节点的右子树
res[node.idx] += root.count + 1; // 本处代码原理请看题目解析中的图示
root.right = insertNode(root.right, node, res); // 递归进入右子树继续比较
}
return root;
}
function getResult(n, levels) {
let root = null;
// rightSmaller[i] 记录的是 levels[i] 右边比自己小的元素的个数
const rightSmaller = new Array(n).fill(0);
for (let i = n - 1; i >= 0; i--) {
root = insertNode(root, new Node(i, levels[i]), rightSmaller);
}
levels.reverse();
root = null;
// leftSmaller[i] 记录的是 levels[i] 左边比自己小的元素的个数
const leftSmaller = new Array(n).fill(0);
for (let i = n - 1; i >= 0; i--) {
root = insertNode(root, new Node(i, levels[i]), leftSmaller);
}
leftSmaller.reverse();
// 统计各个元素: 左小 * 右大 + 左大 * 右小
let sum = 0;
for (let i = 0; i < n; i++) {
// 由于本题中每个员工有独一无二的职级,即levels中所有元素值都不互相相同
const leftSmallerCount = leftSmaller[i];
// 索引i的左边有 i 个元素,而索引i的左边有leftSmallerCount个比自己小的,因此剩余 i - leftSmallerCount 都是比自己大的
const leftBiggerCount = i - leftSmallerCount;
const rightSmallerCount = rightSmaller[i];
// 索引i右边有 n-i-1 个元素,而索引i的右边有rightSmallerCount比自己小的,因此剩余 n-i-1-rightSmallerCount 都是比自己大的
const rightBiggerCount = n - i - 1 - rightSmallerCount;
sum +=
leftSmallerCount * rightBiggerCount + leftBiggerCount * rightSmallerCount;
}
return sum;
}
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());
int[] levels = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
System.out.println(getResult(n, levels));
}
static class Node {
int idx; // 当前节点的值在原数组中的索引
int val; // 当前节点的值
Node left; // 当前节点的左子节点
Node right; // 当前节点的右子节点
int count; // 当前节点的左子树中节点数量
public Node(int idx, int val) {
this.idx = idx;
this.val = val;
}
}
/**
* 向二叉搜索树中插入新节点
*
* @param root (树/子树)根节点
* @param node 要插入的新节点
* @param res 数组,其中res[i]代表第i个节点右边比自己小的元素的个数
* @return 根节点
*/
public static Node insertNode(Node root, Node node, int[] res) {
if (root == null) {
return node;
}
// 由于本题中每个员工有独一无二的职级,即levels中所有元素值都不互相相同,因此这里非大即小
if (node.val < root.val) {
// 如果要插入的新节点的值,比根节点小,则插入根节点左子树
root.count++; // 根节点左子树的节点树+1
root.left = insertNode(root.left, node, res); // 递归进入左子树继续比较
} else {
// 如果要插入的新节点的值,比根节点大,则需要插入根节点的右子树
res[node.idx] += root.count + 1; // 本处代码原理请看题目解析中的图示
root.right = insertNode(root.right, node, res); // 递归进入右子树继续比较
}
return root;
}
public static long getResult(int n, int[] levels) {
Node root = null;
// rightSmaller[i] 记录的是 levels[i] 右边比自己小的元素的个数
int[] rightSmaller = new int[n];
for (int i = n - 1; i >= 0; i--) {
root = insertNode(root, new Node(i, levels[i]), rightSmaller);
}
reverse(levels);
root = null;
// leftSmaller[i] 记录的是 levels[i] 左边比自己小的元素的个数
int[] leftSmaller = new int[n];
for (int i = n - 1; i >= 0; i--) {
root = insertNode(root, new Node(i, levels[i]), leftSmaller);
}
reverse(leftSmaller);
// 统计各个元素: 左小 * 右大 + 左大 * 右小
long sum = 0;
for (int i = 0; i < n; i++) {
// 由于本题中每个员工有独一无二的职级,即levels中所有元素值都不互相相同
long leftSmallerCount = leftSmaller[i];
// 索引i的左边有 i 个元素,而索引i的左边有leftSmallerCount个比自己小的,因此剩余 i - leftSmallerCount 都是比自己大的
long leftBiggerCount = i - leftSmallerCount;
long rightSmallerCount = rightSmaller[i];
// 索引i右边有 n-i-1 个元素,而索引i的右边有rightSmallerCount比自己小的,因此剩余 n-i-1-rightSmallerCount 都是比自己大的
long rightBiggerCount = n - i - 1 - rightSmallerCount;
sum += leftSmallerCount * rightBiggerCount + leftBiggerCount * rightSmallerCount;
}
return sum;
}
public static void reverse(int[] nums) {
int l = 0;
int r = nums.length - 1;
while (l < r) {
int tmp = nums[l];
nums[l] = nums[r];
nums[r] = tmp;
l++;
r--;
}
}
}
Python算法源码
class Node:
def __init__(self, idx, val):
self.idx = idx
self.val = val
self.left = None
self.right = None
self.count = 0
def insertNode(root, node, res):
if root is None:
return node
if node.val < root.val:
root.count += 1
root.left = insertNode(root.left, node, res)
else:
res[node.idx] += root.count + 1
root.right = insertNode(root.right, node, res)
return root
# 输入获取
n = int(input())
levels = list(map(int, input().split()))
# 算法入口
def getResult():
root = None
rightSmaller = [0] * n
for i in range(n - 1, -1, -1):
root = insertNode(root, Node(i, levels[i]), rightSmaller)
levels.reverse()
root = None
leftSmaller = [0] * n
for i in range(n - 1, -1, -1):
root = insertNode(root, Node(i, levels[i]), leftSmaller)
leftSmaller.reverse()
total = 0
for i in range(n):
leftSmallerCount = leftSmaller[i]
leftBiggerCount = i - leftSmallerCount
rightSmallerCount = rightSmaller[i]
rightBiggerCount = n - i - 1 - rightSmallerCount
total += leftSmallerCount * rightBiggerCount + leftBiggerCount * rightSmallerCount
return total
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 6000
typedef struct Node {
int idx; // 当前节点的值在原数组中的索引
int val; // 当前节点的值
struct Node *left; // 当前节点的左子节点
struct Node *right; // 当前节点的右子节点
int count; // 当前节点的左子树中节点数量
} Node;
Node *new_Node(int idx, int val) {
Node *node = (Node *) malloc(sizeof(Node));
node->idx = idx;
node->val = val;
node->left = NULL;
node->right = NULL;
node->count = 0;
return node;
}
/**
* 向二叉搜索树中插入新节点
*
* @param root (树/子树)根节点
* @param node 要插入的新节点
* @param res 数组,其中res[i]代表第i个节点右边比自己小的元素的个数
* @return 根节点
*/
Node *insertNode(Node *root, Node *node, int res[]) {
if (root == NULL) {
return node;
}
// 由于本题中每个员工有独一无二的职级,即levels中所有元素值都不互相相同,因此这里非大即小
if (node->val < root->val) {
// 如果要插入的新节点的值,比根节点小,则插入根节点左子树
root->count++; // 根节点左子树的节点树+1
root->left = insertNode(root->left, node, res); // 递归进入左子树继续比较
} else {
// 如果要插入的新节点的值,比根节点大,则需要插入根节点的右子树
res[node->idx] += root->count + 1; // 本处代码原理请看题目解析中的图示
root->right = insertNode(root->right, node, res); // 递归进入右子树继续比较
}
return root;
}
void reverse(int nums[], int nums_size) {
int l = 0;
int r = nums_size - 1;
while (l < r) {
int tmp = nums[l];
nums[l] = nums[r];
nums[r] = tmp;
l++;
r--;
}
}
long getResult(int n, int levels[], int levels_size) {
Node *root = NULL;
// rightSmaller[i] 记录的是 levels[i] 右边比自己小的元素的个数
int rightSmaller[MAX_SIZE] = {0};
for (int i = n - 1; i >= 0; i--) {
root = insertNode(root, new_Node(i, levels[i]), rightSmaller);
}
reverse(levels, levels_size);
root = NULL;
// leftSmaller[i] 记录的是 levels[i] 左边比自己小的元素的个数
int leftSmaller[MAX_SIZE] = {0};
for (int i = n - 1; i >= 0; i--) {
root = insertNode(root, new_Node(i, levels[i]), leftSmaller);
}
reverse(leftSmaller, levels_size);
// 统计各个元素: 左小 * 右大 + 左大 * 右小
long sum = 0;
for (int i = 0; i < n; i++) {
// 由于本题中每个员工有独一无二的职级,即levels中所有元素值都不互相相同
int leftSmallerCount = leftSmaller[i];
// 索引i的左边有 i 个元素,而索引i的左边有leftSmallerCount个比自己小的,因此剩余 i - leftSmallerCount 都是比自己大的
int leftBiggerCount = i - leftSmallerCount;
int rightSmallerCount = rightSmaller[i];
// 索引i右边有 n-i-1 个元素,而索引i的右边有rightSmallerCount比自己小的,因此剩余 n-i-1-rightSmallerCount 都是比自己大的
int rightBiggerCount = n - i - 1 - rightSmallerCount;
sum += leftSmallerCount * rightBiggerCount + leftBiggerCount * rightSmallerCount;
}
return sum;
}
int main() {
int n;
scanf("%d", &n);
int levels[MAX_SIZE];
int levels_size = 0;
while (scanf("%d", &levels[levels_size++])) {
if (getchar() != ' ') break;
}
printf("%ldn", getResult(n, levels, levels_size));
return 0;
}免责声明:
评论0