题目描述
假定街道是棋盘型的,每格距离相等,车辆通过每格街道需要时间均为 timePerRoad;
街道的街口(交叉点)有交通灯,灯的周期 T(=lights[row][col])各不相同;
车辆可直行、左转和右转,其中直行和左转需要等相应 T 时间的交通灯才可通行,右转无需等待。
现给出 n * m 个街口的交通灯周期,以及起止街口的坐标,计算车辆经过两个街口的最短时间。
其中:
- 起点和终点的交通灯不计入时间,且可以在任意方向经过街口
- 不可超出 n * m 个街口,不可跳跃,但边线也是道路(即:lights[0][0] -> lights[0][1] 是有效路径)
入口函数定义:
/** * @param lights:n*m个街口每个交通灯的周期,值范围[0, 120],n和m的范围为[1,9] * @param timePreRoad:相邻两个街口之间街道的通行时间,范围为[0,600] * @param rowStart:起点的行号 * @param colStart:起点的列号 * @param rowEnd:终点的行号 * @param colEnd:终点的列号 * @return lights[rowStart][colStart] 与 lights[rowEnd][colEnd] 两个街口之间的最短通行时间 */ int calcTime(int[][] lights, int timePreRoad, int rowStart, int colStart, int rowEnd, int colEnd)
输入描述
第一行输入 n 和 m,以空格分隔
之后 n 行输入 lights矩阵,矩阵每行m个整数,以空格分隔
之后一行输入 timePerRoad
之后一行输入 rowStart colStart,以空格分隔
最后一行输入 rowEnd colEnd,以空格分隔
输出描述
lights[rowStart][colStart] 与 lights[rowEnd][colEnd] 两个街口之间的最短通行时间
用例
| 输入 | 3 3 1 2 3 4 5 6 7 8 9 60 0 0 2 2 |
| 输出 | 245 |
| 说明 | 行走路线为 (0,0) -> (0,1) -> (1,1) -> (1,2) -> (2,2) 走了4格路,2个右转,1个左转,共耗时 60+0+60+5+60+0+60=245 |
题目解析
用例图示如下:
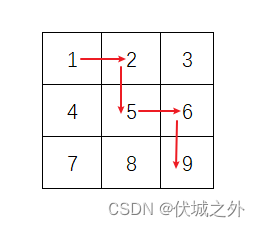
(0,0)是起点,(2,2)是终点
上面红色路径是起点到终点的最短时间路径,各线段花费时间如下:
- (0,0) → (0,1) 由于是初始,因此不需要等待,仅花费 timePerRoad = 60 单位时间
- (0,1) → (1,1) 发生了右拐,因此不需要等待,仅花费 timePerRoad = 60 单位时间
- (1,1) → (1,2) 发生了左拐,因此需要等待,花费时间为 timePerRoad + lights[1][1] = 60 + 5 单位时间
- (1,2) → (2,2) 发生了右拐,因此不需要等待,仅花费 timePerRoad = 60 单位时间
最终总耗时为:60 + 60 + (60 + 5) + 60 = 245
本题看上去是单源最短路径问题,但是实际操作起来是不可以的,
比如基于题目用例,我们通过Dijistra算法模拟,过程如下:
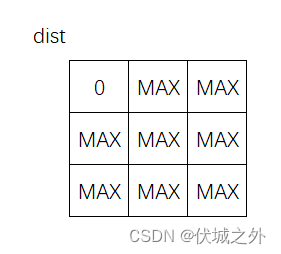
初始定义一个dist数组,dist[i][j]用于记录 起点 到 (i, j)点 的最短时间。
初始时,起点到达自身位置的时间为0,到达其余点的时间为无限大MAX,如下图所示:
然后我们从起点出发,此时可以向上下左右四个方向探索:
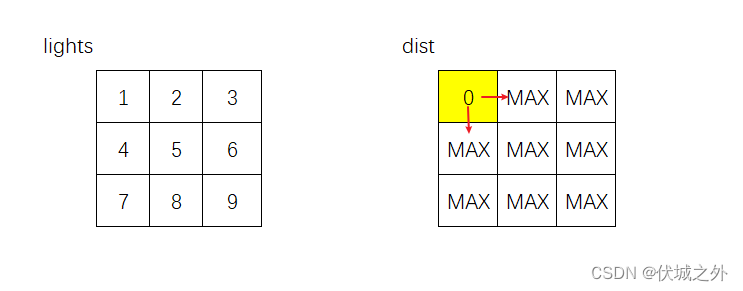
由于探索位置不能越界,因此当前用例起点只能向下和向右探索,由于是初始探索,因此不需要等待,到达新位置只需要花费timePerRoad时间
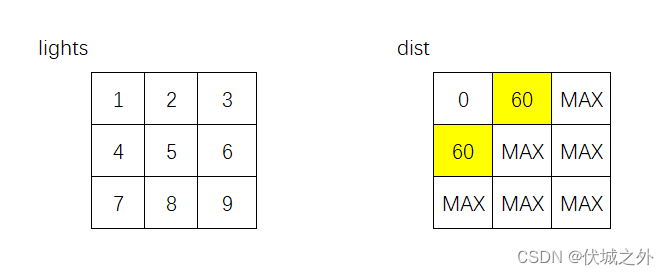
接下来有两个点可以当成新的源点,根据Dijistra算法,我们可以选择其中较小权重(时间)的点作为源点,此时由于两点权重(时间)相同,因此任选一个都可以
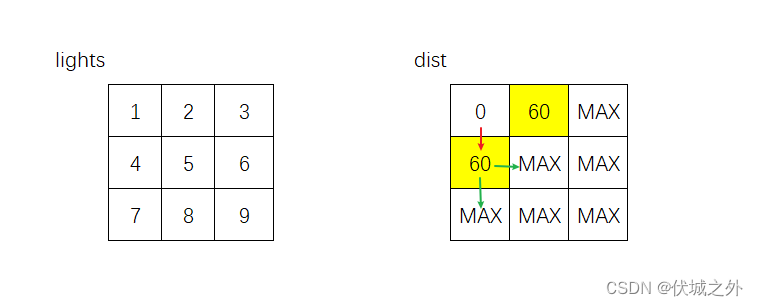
比如我们选择(1,0)点作为新的源点,此时该点可以向下和向右探索:
- 向下的话,则是直线运动,需要等待,此时需要花费 timePerRod + lights[1][1] 的时间
- 向右的话,则是左转运动,需要等待,此时需要花费 timePerRod + lights[1][1] 的时间
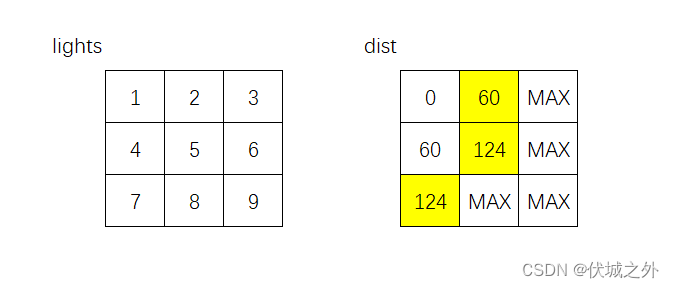
接下来,需要从124,124,60中选择最小的60作为源点进行探索,该点只能向右和向下探索
- 向右的话,则是直线运动,需要等待,此时需要花费 timePerRod + lights[0][1] 的时间
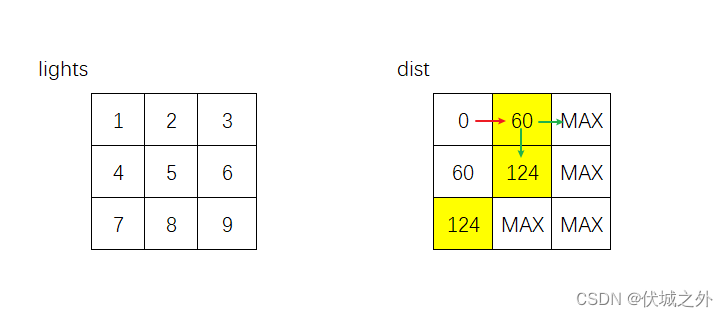
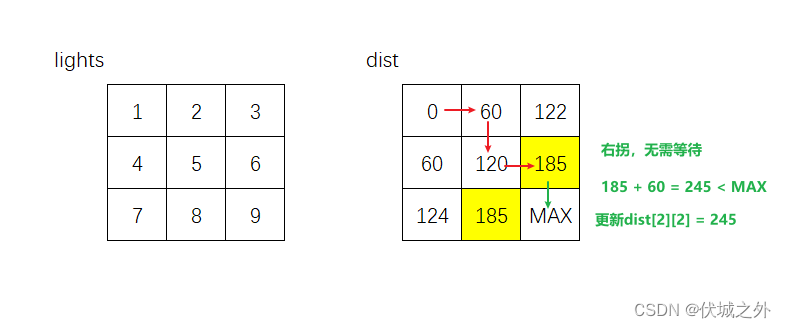
- 向下的话,则是右转运动,不需要等待,此时仅需要花费 timePerRod 时间,即起点(0,0)到达(1,1)沿当前路径只需要120时间,要比之前探索的124小,根据Dijistra算法,更新dist[]
接下来,需要从124,120,122中选择最小的120作为源点进行探索,该点只能向右和向下探索
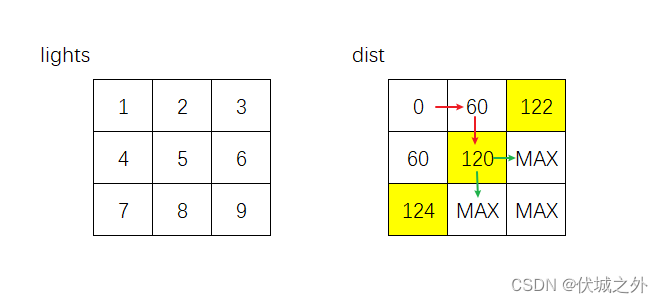
- 向右的话,则是左转运动,需要等待,此时需要花费 timePerRod + lights[1][1] 的时间
- 向下的话,则是直线运动,需要等待,此时需要花费 timePerRod + lights[1][1] 的时间
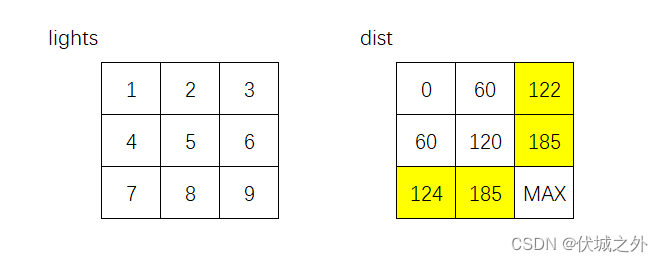
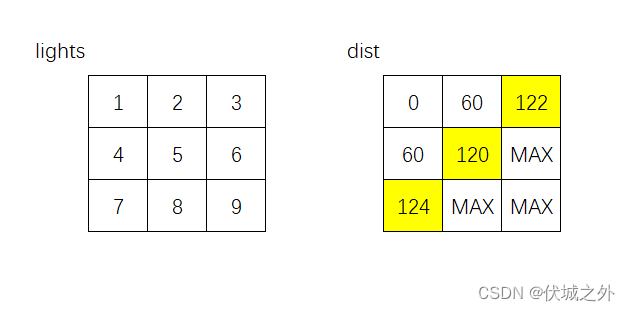
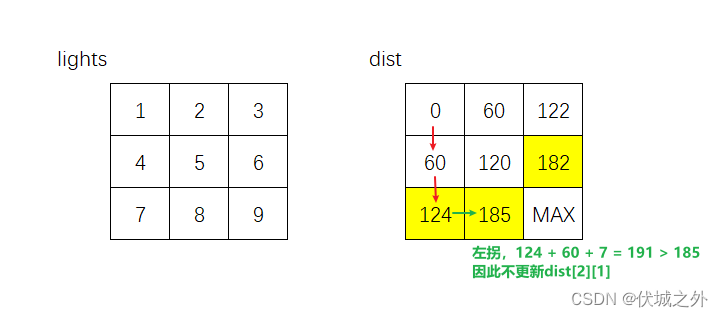
接下来,需要从124,122,185,185中选择最小的122作为源点进行探索,该点只能向下探索
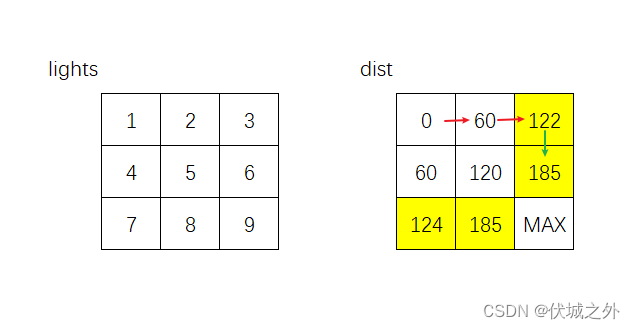
向右的话,则是右转运动,不需要等待,仅需要花费 timePerRod 时间,此时起点到达(1, 2)位置需要122+60 = 182时间,要比(1,2)当前记录的185时间更短,因此根据Dijistra算法,会更新dist[1][2] = 182,但是此时就会出问题!!!!
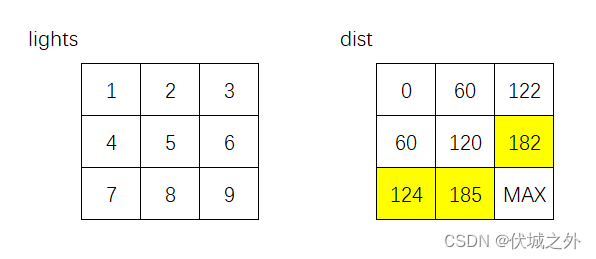
我们快速走完后续流程,看下结果:
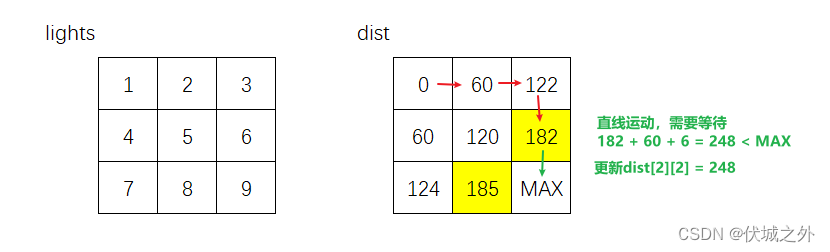
即按照Dijistra算法的逻辑,最终起点(0,0)到终点(2,2)的最短时间为248,但是这是有问题的,我们回到之前锚定问题的状态:

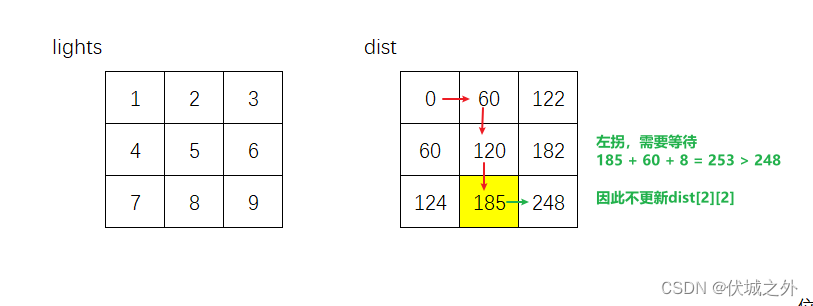
如果上面绿色箭头选择不更新(1,2)位置的时间的话,即保持dist[1][2] = 185,那么结果如下:
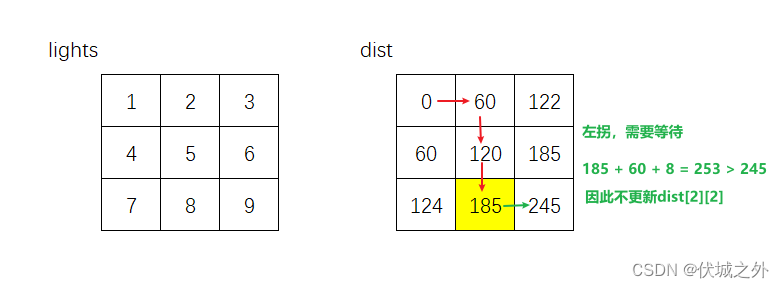
最终起点(0,0)到终点(2,2)的最短时间为245,相较于Dijistra算法得出的最优选择,时间更短。
本题的街道本质上,是一个动态边权的有权图,两个点之间的边权,会因为第三个点的加入而改变,因此边权是动态的。而Dijistra算法无法处理这种情况。
我理解,本题只能进行暴力搜索所有起点到终点的路径,并根据拐弯规则计算动态边权,得出最短时间的路径。
本题的n和m的范围为[1,9],不是很大,因此暴力搜索(如DFS)应该不会超时。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
const [n, m] = (await readline()).split(" ").map(Number);
const lights = [];
for (let i = 0; i < n; i++) {
lights.push((await readline()).split(" ").map(Number));
}
const timePerRoad = parseInt(await readline());
const [rowStart, colStart] = (await readline()).split(" ").map(Number);
const [rowEnd, colEnd] = (await readline()).split(" ").map(Number);
// 记录访问过的点,防止走回路
const visited = new Array(n).fill(0).map(() => new Array(m).fill(false));
const offsets = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1],
];
function getResult() {
// 初始时起点位置标记为访问过
visited[rowStart][colStart] = true;
// 记录起点到终点的最小花费时间,这里minCost定义为数组,是为了其在dfs函数调用结束后,不会被释放内存,因为它是引用类型变量
const minCost = [Infinity];
// 开始暴搜所有起点到终点的路径
dfs(rowStart, colStart, -1, -1, 0, minCost);
return minCost[0];
}
/**
* 暴力搜索
*
* @param curX 当前位置横坐标
* @param curY 当前位置纵坐标
* @param preX 上一个位置横坐标
* @param preY 上一个位置纵坐标
* @param cost 到达当前位置花费的时间
* @param minCost 记录起点到终点的最小花费时间
*/
function dfs(curX, curY, preX, preY, cost, minCost) {
// 如果到达当前前花费的时间cost 达到了 已知minCost,那么后续路径就没必要探索了,因为必然要比minCost大
if (cost >= minCost[0]) {
return;
}
// 如果当前点是终点,且花费的时间cost更少,则更新minCost
if (curX == rowEnd && curY == colEnd) {
minCost[0] = cost;
return;
}
// 否则,从当前位置的四个方向继续探索路径
for (let [offsetX, offsetY] of offsets) {
// 新位置
const nextX = curX + offsetX;
const nextY = curY + offsetY;
// 新位置越界或者已经访问过,则不能访问,继续其他方向探索
if (
nextX < 0 ||
nextX >= n ||
nextY < 0 ||
nextY >= m ||
visited[nextX][nextY]
)
continue;
// 标记新位置访问过
visited[nextX][nextY] = true;
// 根据pre,cur,next三点,判断拐弯方向
const direction = getDirection(preX, preY, curX, curY, nextX, nextY);
// cur到达next位置必须要增加timePreRoad个时间
let increment = timePerRoad;
// preX=-1, preY=-1 表示pre位置不存在,此时探索下一个位置不需要花费等待周期
if (preX >= 0 && preY >= 0 && direction >= 0) {
// pre位置存在,且cur->next是左拐或者直行,则需要增加当前位置对应的等待周期时间
increment += lights[curX][curY];
}
// 递归进入新位置
dfs(nextX, nextY, curX, curY, cost + increment, minCost);
// 回溯
visited[nextX][nextY] = false;
}
}
/**
* 根据三点坐标,确定拐弯方向
*
* @param preX 前一个点横坐标
* @param preY 前一个点纵坐标
* @param curX 当前点横坐标
* @param curY 当前点纵坐标
* @param nextX 下一个点横坐标
* @param nextY 下一个点纵坐标
* @return cur到next的拐弯方向, >0 表示向左拐, ==0 表示直行(含调头), <0 表示向右拐
*/
function getDirection(preX, preY, curX, curY, nextX, nextY) {
// 向量 pre->cur
const dx1 = curX - preX;
const dy1 = curY - preY;
// 向量 cur->next
const dx2 = nextX - curX;
const dy2 = nextY - curY;
// 两个向量的叉积 >0 表示向左拐, ==0 表示直行(含调头), <0 表示向右拐
return dx1 * dy2 - dx2 * dy1;
}
console.log(getResult());
})();
Java算法源码
import java.util.Scanner;
public class Main {
static int n;
static int m;
static int[][] lights;
static int timePreRoad;
static int rowStart;
static int colStart;
static int rowEnd;
static int colEnd;
static boolean[][] visited;
static int[][] offsets = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
lights = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
lights[i][j] = sc.nextInt();
}
}
timePreRoad = sc.nextInt();
rowStart = sc.nextInt();
colStart = sc.nextInt();
rowEnd = sc.nextInt();
colEnd = sc.nextInt();
System.out.println(getResult());
}
public static int getResult() {
// 记录访问过的点,防止走回路
visited = new boolean[n][m];
// 初始时起点位置标记为访问过
visited[rowStart][colStart] = true;
// 记录起点到终点的最小花费时间,这里minCost定义为数组,是为了其在dfs函数调用结束后,不会被释放内存,因为它是引用类型变量
int[] minCost = {Integer.MAX_VALUE};
// 开始暴搜所有起点到终点的路径
dfs(rowStart, colStart, -1, -1, 0, minCost);
return minCost[0];
}
/**
* 暴力搜索
*
* @param curX 当前位置横坐标
* @param curY 当前位置纵坐标
* @param preX 上一个位置横坐标
* @param preY 上一个位置纵坐标
* @param cost 到达当前位置花费的时间
* @param minCost 记录起点到终点的最小花费时间
*/
public static void dfs(int curX, int curY, int preX, int preY, int cost, int[] minCost) {
// 如果到达当前前花费的时间cost 达到了 已知minCost,那么后续路径就没必要探索了,因为必然要比minCost大
if (cost >= minCost[0]) {
return;
}
// 如果当前点是终点,且花费的时间cost更少,则更新minCost
if (curX == rowEnd && curY == colEnd) {
minCost[0] = cost;
return;
}
// 否则,从当前位置的四个方向继续探索路径
for (int[] offset : offsets) {
// 新位置
int nextX = curX + offset[0];
int nextY = curY + offset[1];
// 新位置越界或者已经访问过,则不能访问,继续其他方向探索
if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m || visited[nextX][nextY]) continue;
// 标记新位置访问过
visited[nextX][nextY] = true;
// 根据pre,cur,next三点,判断拐弯方向
int direction = getDirection(preX, preY, curX, curY, nextX, nextY);
// cur到达next位置必须要增加timePreRoad个时间
int increment = timePreRoad;
// preX=-1, preY=-1 表示pre位置不存在,此时探索下一个位置不需要花费等待周期
if (preX >= 0 && preY >= 0 && direction >= 0) {
// pre位置存在,且cur->next是左拐或者直行,则需要增加当前位置对应的等待周期时间
increment += lights[curX][curY];
}
// 递归进入新位置
dfs(nextX, nextY, curX, curY, cost + increment, minCost);
// 回溯
visited[nextX][nextY] = false;
}
}
/**
* 根据三点坐标,确定拐弯方向
*
* @param preX 前一个点横坐标
* @param preY 前一个点纵坐标
* @param curX 当前点横坐标
* @param curY 当前点纵坐标
* @param nextX 下一个点横坐标
* @param nextY 下一个点纵坐标
* @return cur到next的拐弯方向, >0 表示向左拐, ==0 表示直行(含调头), <0 表示向右拐
*/
public static int getDirection(int preX, int preY, int curX, int curY, int nextX, int nextY) {
// 向量 pre->cur
int dx1 = curX - preX;
int dy1 = curY - preY;
// 向量 cur->next
int dx2 = nextX - curX;
int dy2 = nextY - curY;
// 两个向量的叉积 >0 表示向左拐, ==0 表示直行(含调头), <0 表示向右拐
return dx1 * dy2 - dx2 * dy1;
}
}
Python算法源码
import sys
# 输入获取
n, m = map(int, input().split())
lights = [list(map(int, input().split())) for _ in range(n)]
timePerRoad = int(input())
rowStart, colStart = map(int, input().split())
rowEnd, colEnd = map(int, input().split())
offsets = ((-1, 0), (1, 0), (0, -1), (0, 1))
visited = [[False] * m for _ in range(n)]
# 根据三点坐标,确定拐弯方向
def getDirection(preX, preY, curX, curY, nextX, nextY):
"""
:param preX: 前一个点横坐标
:param preY: 前一个点纵坐标
:param curX: 当前点横坐标
:param curY: 当前点纵坐标
:param nextX: 下一个点横坐标
:param nextY: 下一个点纵坐标
:return: cur到next的拐弯方向, >0 表示向左拐, ==0 表示直行(含调头), <0 表示向右拐
"""
# 向量 pre->cur
dx1 = curX - preX
dy1 = curY - preY
# 向量 cur->next
dx2 = nextX - curX
dy2 = nextY - curY
# 两个向量的叉积 >0 表示向左拐, ==0 表示直行(含调头), <0 表示向右拐
return dx1 * dy2 - dx2 * dy1
# 暴力搜索
def dfs(curX, curY, preX, preY, cost, minCost):
"""
:param curX: 当前位置横坐标
:param curY: 当前位置纵坐标
:param preX: 上一个位置横坐标
:param preY: 上一个位置纵坐标
:param cost: 到达当前位置花费的时间
:param minCost: 记录起点到终点的最小花费时间
"""
# 如果到达当前前花费的时间cost 达到了 已知minCost,那么后续路径就没必要探索了,因为必然要比minCost大
if cost >= minCost[0]:
return
# 如果当前点是终点,且花费的时间cost更少,则更新minCost
if curX == rowEnd and curY == colEnd:
minCost[0] = cost
return
# 否则,从当前位置的四个方向继续探索路径
for offsetX, offsetY in offsets:
# 新位置
nextX = curX + offsetX
nextY = curY + offsetY
# 新位置越界或者已经访问过,则不能访问,继续其他方向探索
if nextX < 0 or nextX >= n or nextY < 0 or nextY >= m or visited[nextX][nextY]:
continue
# 标记新位置访问过
visited[nextX][nextY] = True
# 根据pre,cur,next三点,判断拐弯方向
direction = getDirection(preX, preY, curX, curY, nextX, nextY)
# cur到达next位置必须要增加timePreRoad个时间
increment = timePerRoad
# preX=-1, preY=-1 表示pre位置不存在,此时探索下一个位置不需要花费等待周期
if preX >= 0 and preY >= 0 and direction >= 0:
# pre位置存在,且cur->next是左拐或者直行,则需要增加当前位置对应的等待周期时间
increment += lights[curX][curY]
# 递归进入新位置
dfs(nextX, nextY, curX, curY, cost + increment, minCost)
# 回溯
visited[nextX][nextY] = False
# 算法入口
def getResult():
visited[rowStart][colStart] = True
minCost = [sys.maxsize]
dfs(rowStart, colStart, -1, -1, 0, minCost)
return minCost[0]
# 算法调用
print(getResult())
C算法源码
#include <stdio.h>
#include <limits.h>
#define MAX_SIZE 10
int n, m;
int lights[MAX_SIZE][MAX_SIZE];
int timePerRoad;
int rowStart, colStart;
int rowEnd, colEnd;
int offsets[4][2] = {{-1, 0},
{1, 0},
{0, -1},
{0, 1}};
int visited[MAX_SIZE][MAX_SIZE] = {0};
/*!
* 根据三点坐标,确定拐弯方向
* @param preX 前一个点横坐标
* @param preY 前一个点纵坐标
* @param curX 当前点横坐标
* @param curY 当前点纵坐标
* @param nextX 下一个点横坐标
* @param nextY 下一个点纵坐标
* @return cur到next的拐弯方向, >0 表示向左拐, ==0 表示直行(含调头), <0 表示向右拐
*/
int getDirection(int preX, int preY, int curX, int curY, int nextX, int nextY) {
// 向量 pre->cur
int dx1 = curX - preX;
int dy1 = curY - preY;
// 向量 cur->next
int dx2 = nextX - curX;
int dy2 = nextY - curY;
// 两个向量的叉积 >0 表示向左拐, ==0 表示直行(含调头), <0 表示向右拐
return dx1 * dy2 - dx2 * dy1;
}
/*!
* 暴力搜索
* @param curX 当前位置横坐标
* @param curY 当前位置纵坐标
* @param preX 上一个位置横坐标
* @param preY 上一个位置纵坐标
* @param cost 到达当前位置花费的时间
* @param minCost 记录起点到终点的最小花费时间
*/
void dfs(int curX, int curY, int preX, int preY, int cost, int minCost[]) {
// 如果到达当前前花费的时间cost 达到了 已知minCost,那么后续路径就没必要探索了,因为必然要比minCost大
if (cost >= minCost[0]) {
return;
}
// 如果当前点是终点,且花费的时间cost更少,则更新minCost
if (curX == rowEnd && curY == colEnd) {
minCost[0] = cost;
return;
}
// 否则,从当前位置的四个方向继续探索路径
for (int i = 0; i < 4; i++) {
// 新位置
int nextX = curX + offsets[i][0];
int nextY = curY + offsets[i][1];
// 新位置越界或者已经访问过,则不能访问,继续其他方向探索
if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m || visited[nextX][nextY]) {
continue;
}
// 标记新位置访问过
visited[nextX][nextY] = 1;
// 根据pre,cur,next三点,判断拐弯方向
int direction = getDirection(preX, preY, curX, curY, nextX, nextY);
// cur到达next位置必须要增加timePreRoad个时间
int increment = timePerRoad;
// preX=-1, preY=-1 表示pre位置不存在,此时探索下一个位置不需要花费等待周期
if (preX >= 0 && preY >= 0 && direction >= 0) {
// pre位置存在,且cur->next是左拐或者直行,则需要增加当前位置对应的等待周期时间
increment += lights[curX][curY];
}
// 递归进入新位置
dfs(nextX, nextY, curX, curY, cost + increment, minCost);
// 回溯
visited[nextX][nextY] = 0;
}
}
int getResult() {
// 记录访问过的点,防止走回路
// 初始时起点位置标记为访问过
visited[rowStart][colStart] = 1;
// 记录起点到终点的最小花费时间,这里minCost定义为数组,是为了其在dfs函数调用结束后,不会被释放内存,因为它是引用类型变量
int minCost[] = {INT_MAX};
// 开始暴搜所有起点到终点的路径
dfs(rowStart, colStart, -1, -1, 0, minCost);
return minCost[0];
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
scanf("%d", &lights[i][j]);
}
}
scanf("%d", &timePerRoad);
scanf("%d %d", &rowStart, &colStart);
scanf("%d %d", &rowEnd, &colEnd);
printf("%dn", getResult());
return 0;
}免责声明:
评论0