题目描述
你有 n 台机器,编号为 1~n,每台都需要完成一项工作,机器经过配置后都能独立完成一项工作。
假设第 i 台机器你需要花 Bi 分钟进行设置,然后开始运行,Ji 分钟后完成任务。
现在,你需要选择布置工作的顺序,使得用最短的时间完成所有工作。
注意,不能同时对两台进行配置,但配置完成的机器们可以同时执行他们各自的工作。
输入描述
第一行输入代表总共有 M 组任务数据(1<M<=10)。
每组数第一行为一个整数指定机器的数量 N(0<N<=1000)。随后的 N 行每行两个整数,第一个表示 B(0<=B<=10000),第二个表示 J(0<=J<=10000)。
每组数据连续输入,不会用空行分隔。各组任务单独计时。
输出描述
对于每组任务,输出最短完成时间,且每组的结果独占一行。例如,两组任务就应该有两行输出。
用例
| 输入 | 1 1 2 2 |
| 输出 | 4 |
| 说明 | 输入共3行数据, 第一行代表只有1组任务; 第二行代表本组任务只有1台机器; 第三行代表本机器:配置需要2分钟,执行任务需要2分钟, 输出共一行数据,代表执行结果为4分钟 |
| 输入 | 2 2 1 1 2 2 3 1 1 2 2 3 3 |
| 输出 | 4 7 |
| 说明 | 第1行 2代表有2组任务; 2~4行代表第1组数据,为2台机器的配置、执行信息 第1台:配置1分钟,执行1分钟 第2台:配置2分钟,执行2分钟 5~8行代表第2组数据,为3台机器的配置、执行信息 输出共2行,分别代表第1组任务共需要4分钟和第2组任务共需要7分钟 |
题目解析
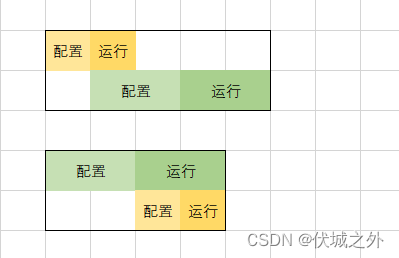
如上图是两个机器执行的两种方案,我们可以发现:绿色机器先执行的话,总用时最少。
因为,绿色机器的运行时间更长,而橙色机器可以在绿色机器运行过程中完成配置和执行。
得出结论:如果想让任务总用时最少,则优先配置”运行时间长”的机器。
那么,如果两个机器的运行时间相同,但是配置时间不同呢?
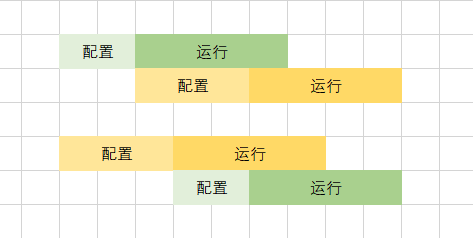
可以发现,两种配置方式的总用时是相同的。
得出结论:如果两个机器运行时间相同,则谁先配置都可以,对结果总用时无影响。
因此,对各个机器进行配置先后优先级排序后,再算出每个机器的配置结束时间
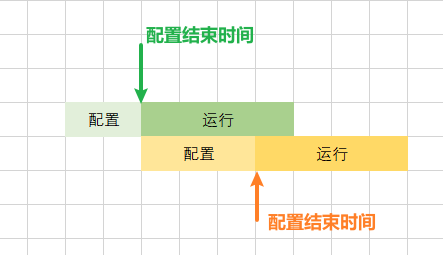
此时,总用时 = max(“每个机器的配置结束时间 + 该机器的运行时间“)
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void (async function () {
// Write your code here
const m = (await readline()) - 0; // 获取总任务数m
const tasks = [];
// 循环m次,每次获取一个任务下的机器详情
for (let i = 0; i < m; i++) {
const n = (await readline()) - 0; //获取机器数n
const machines = [];
//循环n次,每次获取一个机器的 配置时间、运行时间
for (let j = 0; j < n; j++) {
const machine = await readline(); // 获取机器的 配置时间、运行时间
machines.push(machine.split(" ").map(Number));
}
// tasks中存放的是task,每个task下又存放多个机器信息,每个机器信息包括:配置时间、运行时间
tasks.push(machines);
}
// 业务逻辑
for (let task of tasks) {
// 将每个任务中的机器工作顺序,按照运行时间降序排序
task.sort((a, b) => b[1] - a[1]);
let config_endTime = 0;
let ans = 0;
for (let [config_cost, run_cost] of task) {
config_endTime += config_cost;
ans = Math.max(ans, config_endTime + run_cost);
}
console.log(ans);
}
})();
Java算法源码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
// 输入获取
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
int[][][] tasks = new int[m][][];
for (int i = 0; i < m; i++) {
int n = sc.nextInt();
int[][] task = new int[n][2];
for (int j = 0; j < n; j++) {
task[j][0] = sc.nextInt();
task[j][1] = sc.nextInt();
}
tasks[i] = task;
}
getResult(tasks);
}
// 算法入口
public static void getResult(int[][][] tasks) {
for (int[][] task : tasks) {
// 将每个任务中的机器工作顺序,按照运行时间降序排序
Arrays.sort(task, (a, b) -> b[1] - a[1]);
int config_endTime = 0;
int ans = 0;
for (int[] info : task) {
int config_cost = info[0];
int run_cost = info[1];
config_endTime += config_cost;
ans = Math.max(ans, config_endTime + run_cost);
}
System.out.println(ans);
}
}
}
Python算法源码
# 输入获取
m = int(input())
tasks = [[] for _ in range(m)]
for i in range(m):
n = int(input())
task = [[] for _ in range(n)]
for j in range(n):
task[j] = list(map(int, input().split()))
tasks[i] = task
# 算法入口
def getResult():
for task in tasks:
# 将每个任务中的机器工作顺序,按照运行时间降序排序
task.sort(key=lambda x: -x[1])
config_endTime = 0
ans = 0
for config_cost, run_cost in task:
config_endTime += config_cost
ans = max(ans, config_endTime + run_cost)
print(ans)
# 算法调用
getResult()
C算法源码
#include <stdio.h>
#include <stdlib.h>
#define MAX(a, b) ((a) > (b) ? (a) : (b))
typedef struct {
int config_cost;
int run_cost;
} Task;
int cmp(const void *a, const void *b) {
return ((Task *) b)->run_cost - ((Task *) a)->run_cost;
}
int main() {
// 总共有 M 组任务数据
int m;
scanf("%d", &m);
for (int i = 0; i < m; i++) {
// 机器的数量 N
int n;
scanf("%d", &n);
Task *tasks = (Task *) malloc(sizeof(Task) * n);
for (int j = 0; j < n; j++) {
// 配置时间,运行时间
scanf("%d %d", &tasks[j].config_cost, &tasks[j].run_cost);
}
// 将每个任务中的机器工作顺序,按照运行时间降序排序
qsort(tasks, n, sizeof(Task), cmp);
int config_endTime = 0;
int ans = 0;
// 总用时 = max("每个机器的配置结束时间 + 该机器的运行时间")
for (int j = 0; j < n; j++) {
config_endTime += tasks[j].config_cost;
ans = MAX(ans, config_endTime + tasks[j].run_cost);
}
printf("%dn", ans);
}
return 0;
}
免责声明:
评论0